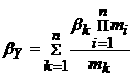Лекции по системному анализу в чрезвычайных ситуациях. Часть 2
- Лекции по системному анализу в чрезвычайных ситуациях. Часть 2
- 6.1. Расплывчатая неопределенность
- 6.1.2 Некоторые понятия теории расплывчатых множеств
- 6.1.3 Функция принадлежности.
- 6.1.4. Нечеткие числа и их использование при моделировании систем
- Лекция 7. Процедуры системного анализа. Структурный анализ и декомпозиция.
- 7.2. Понятие о структурном анализе
- 7.3. Методы декомпозиции
- 7.4. Требования, предъявляемые к декомпозиции
- 7.5. Алгоритм декомпозиции
- 7.6. Программно-целевой подход к решению системных задач
- Лекция 8. Сочетание анализа и синтеза в системных исследованиях. Агрегирование систем.
- 8.2. Виды связей в системе
- 8.3. Виды агрегирования
- Лекция 9. Элементы теории управления
- 9.1.Аксиомы теории управления
- 9.2. Принцип необходимого разнообразия
Известно, что в процессе прогнозирования безопасности разрабатываемых производственных процессов, как правило, ощущается дефицит данных о надежности оборудования, вероятностях ошибок персонала, частоте неблагоприятных воздействий окружающей среды. Это обусловлено как отсутствием соответствующих статистических данных, так и значительной дисперсией имеющихся данных (недостаточной достоверностью). Таким образом, возникает необходимость представления таких данных не точно известными, а приближенными величинами, заданными на некоторых интервалах возможных значений. Здесь теория нечетких множеств может быть весьма полезной, поскольку позволяет заменить точечные оценки вероятностей их интервальными оценками, выраженными в форме нечетких чисел.
Под нечеткой (расплывчатой) величиной N подразумевается подмножество, определяемое на множестве действительных чисел и характеризуемое заданным соответствием между конкретными их значениями и значениями их функции принадлежности (степенями принадлежности) m из интервала [0,1].
Функция принадлежности значений такой величины рассматривается как распределение возможностей появления определенных действительных чисел.
Модальными значениями нечеткой величины — mN являются те элементы множества, которые обладают единичной степенью принадлежности — наибольшей возможностью наблюдения в рассматриваемых условиях: mN(m)=1.
Теперь можно конкретизировать определение нечеткого числа следующим образом.
Нечеткое число — есть полунепрерывный сверху, компактный нечеткий интервал с выпуклой функцией принадлежности и единственным модальным значением.
Это понятие обычно выражается словами «приблизительно, примерно, около, порядка m».
По определению функция принадлежности может иметь несколько форм, отличающихся различным размахом, т.е. шириной диапазона возможных значений действительных чисел. При неограниченном уменьшении размаха, нечеткое число превращается в четкую, фиксированную величину.
 Здесь стоит обратить внимание на сходство между возможностной и вероятностной интерпретациями переменных. Оно проявляется, прежде всего в том, что размах нечеткого числа аналогичен области тех значений случайной величины, на которых совокупная вероятность ее появления равна единице. Однако максимальное значение функции m(m)=1 относится не ко всему нечеткому интервалу, а только к модальному значению действительного числа (по определению).
Здесь стоит обратить внимание на сходство между возможностной и вероятностной интерпретациями переменных. Оно проявляется, прежде всего в том, что размах нечеткого числа аналогичен области тех значений случайной величины, на которых совокупная вероятность ее появления равна единице. Однако максимальное значение функции m(m)=1 относится не ко всему нечеткому интервалу, а только к модальному значению действительного числа (по определению).
Выше было сказано, что над расплывчатыми множествами можно производить действия, соответствующие алгебраическим операциям над функциями принадлежности составляющих множеств. Таким образом, и с нечеткими числами можно производить известные алгебраические операции, в том числе используемые в дереве отказов логические сложение и умножение, изменение знака (отрицание). Наиболее просто это делается при предварительной аппроксимации нечетких чисел в так называемой L-R форме («Left-Right»).
По определению функция принадлежности может иметь несколько форм, отличающихся различным размахом a и b, т.е. шириной диапазона возможных значений действительных чисел. Обычно принимают a = b = 0,0556m.
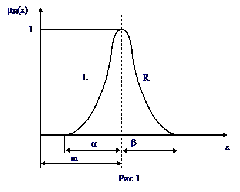
Эта величина получается при допущении, что функции принадлежности нечетких чисел аппроксимируются следующей L-R-формой:
где ai = bI — симметричные относительно модального значения mi коэффициенты размаха i-х нечетких чисел.
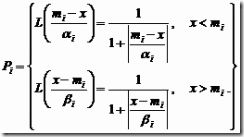
Предполагается также, что величины размаха ее левой L и правой R ветвей изменяются от mPi(xi= mi)=1 для точки их пересечения xi= mi (по определению нечеткого числа) до mPi(xi= mi± 0,5mi)£ 0,1 при отклонениях переменной на половину величины mi , т.е. соблюдается следующее условие:
mPi(xi= 0,5mi) = mPi(xi= mi± 0,5mi)£ 0,1 . (2)
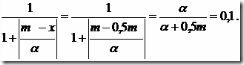
Это можно интерпретировать следующим образом: возможность того, что частота появления исследуемых событий отклоняется от заданных средних значений на 50% равна 0,1. Подставив это значение в 2.1, получим
Отсюда следует, что a = b = 0,0556m.
При неограниченном уменьшении размаха, нечеткое число превращается в четкую, фиксированную величину.
Правила операций над нечеткими числами A = (mA ,a, b ) и B=(mB , g, d) приведены в табл. 2.1.
Табл. 2.1
|
AÅB |
mA+mB , a+b, g+d |
|
mA - mB , a+d, b+g |
|
|
AÄB |
mA × mB , mA g+ mB a+ ag, mAd+ mBb+bd |
Здесь Å,![]() ,Ä — операции сложения, вычитания и перемножения нечетких чисел в L-R-форме
,Ä — операции сложения, вычитания и перемножения нечетких чисел в L-R-форме
Прогноз меры возможности появления головного события PY, образуемого логическим сложением или перемножением n предпосылок, проводится после предварительной аппроксимации их параметров нечеткими числами (m, a b) в форме L-R-диаграммы (рис.2.1).
Обозначим через PY нечеткое число, выражающее меру возможности появления результирующего события, обусловленного событиями Pi.
При связи событий Pi логическим «и» имеем:
причем
При связи событий Pi логическим «или» имеем:
причем
Как приближенные, так и точные количественные параметры исходных предпосылок определяются на основе статистических данных по интенсивности отказов техники, частоте ошибок персонала и вероятности нерасчетных внешних воздействий.
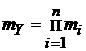
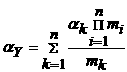
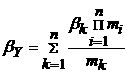
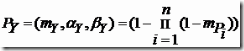
![clip_image012[1] clip_image012[1]](/images/stories/clip_image012-1_thumb.gif)