Лекции по системному анализу в чрезвычайных ситуациях. Часть 2
- Лекции по системному анализу в чрезвычайных ситуациях. Часть 2
- 6.1. Расплывчатая неопределенность
- 6.1.2 Некоторые понятия теории расплывчатых множеств
- 6.1.3 Функция принадлежности.
- 6.1.4. Нечеткие числа и их использование при моделировании систем
- Лекция 7. Процедуры системного анализа. Структурный анализ и декомпозиция.
- 7.2. Понятие о структурном анализе
- 7.3. Методы декомпозиции
- 7.4. Требования, предъявляемые к декомпозиции
- 7.5. Алгоритм декомпозиции
- 7.6. Программно-целевой подход к решению системных задач
- Лекция 8. Сочетание анализа и синтеза в системных исследованиях. Агрегирование систем.
- 8.2. Виды связей в системе
- 8.3. Виды агрегирования
- Лекция 9. Элементы теории управления
- 9.1.Аксиомы теории управления
- 9.2. Принцип необходимого разнообразия
Из аксиом управления следует, что управление заключается в ограничении разнообразия состояний управляемого объекта. Это означает, что энтропия объекта управления должна быть равна нулю Н(Y) = 0. Иными словами, неопределенность относительно состояний объекта управления в управляющей системе должна полностью отсутствовать и объект управления должен находиться в строго определенном состоянии с вероятностью, равной единице.
Если управляемый объект характеризуется одним показателем качества y1 и может находиться в n состояниях y1, y2, y3…. yn с вероятностями p(y1), p(y2)…. p(yn), то сообщение Y о том, в каком из состояний находится объект в системе с полной информацией, будет содержать количество информации, равное его энтропии
Для оценки состояний объекта, характеризуемого m показателями качества y, требуется провести суммирование и по j, j= 1,2, …., m.
Энтропия Н(Y) является мерой первоначальной неопределенности состояния объекта управления. Чем больше число различных состояний объекта и чем меньше отличаются друг от друга их вероятности, тем больше энтропия объекта управления. При n равновероятных состояниях рi = 1/n значение энтропии максимально: Н(Y)max = log2n.
С получением сведений об объекте управления неопределенность его состояния для управляющей системы уменьшается. Количество взаимной информации в сообщениях, предназначенных для уточнения состояния (уменьшения энтропии) объекта управления, определяют как разность:
где Н(Y/Y ‘) — условная энтропия объекта после получения сообщения Y ‘.
Если полученное сообщение полностью характеризует состояние объекта, то оно полностью снимает неопределенность (Н(Y /Y’) = 0) и несет количество информации, равное Н(Y), т.е.
I(Y /Y’) = Н(Y).
Из теории информации также известно, что количество ин формации обладает двумя важными свойствами: положительностью и симметричностью. Первое свойство свидетельствует о том, что количество информации всегда больше или равно нулю (I ³ 0). Согласно второму свойству количество взаимной информации I(А, В), которое содержит принятое сообщение о посланном, равно количеству взаимной информации I(В, А), которое содержит посланное сообщение о принятом
I(А, В) = I(В, А).
Указанные характеристики информации позволяют провес ти анализ управляющих воздействий относительно их соответствия состояниям управляемого объекта. Иначе, определить пределы управления.
Пусть существует система с управлением, в которой решается задача стабилизации — поддержание заданного состояния при случайных воздействиях внешней среды. Система описывается множеством возможных состояний объекта управления Y = {yi}, i = 1,2, … n,
и множеством возможных управляющих воздействий X = {xi}, i = 1,2, … m.
Для определения пределов управления рассмотрим три возможных варианта:
1. Отсутствие управления.
2. Идеальное управление (управление с полной информацией).
3. Реальное управление (управление с неполной информацией).
1. Отсутствие управления. Если управление отсутствует, то управляемый объект может принимать любое из состояний Y и характеризуется максимальной энтропией
2. Идеальное управление. Если управление идеальное, управляемый объект будет все время находиться в заданном состоянии с вероятностью, равной единице, и поэтому энтропия управляемого объекта равна нулю. Действительно, пусть для заданной системы при условии воздействий Х вероятность первого состояния p(y1) = 1, а вероятности остальных состояний ![]() . Следовательно,
. Следовательно,
3. Реальное управление. При управлении в реальных условиях имеют место отклонения состояния управляемого объекта относительно заданного. Это определяется тем, что управляющая система в общем случае подвержена внешним воздействиям, не обладает полной информацией о состоянии среды М и объекта управления Y (N’Ì N и Y’Ì Y). Это приводит к тому, что управляющие воздействия не полностью соответствуют требуемым воз действиям. В этом случае можно сделать вывод, что энтропия объекта управления в реальных условиях может изменяться в пределах
0 < Н(Y/Х) < Н(Y)max .
Качество управления может определяться количеством взаимной информации I (Х, Y) в управляющих воздействиях Х относительно состояний управляемого объекта Y, вычисляемой как разность между безусловной и условной энтропией
Н(Y)max — Н(Y/Х)= I (Х, Y), (1)
что соответствует уменьшению энтропии управляемого объекта на величину, равную полученной информации.
С другой стороны, количество взаимной информации I(X,Y) в управляющих воздействиях Х относительно состояний управляемого объекта Y может быть выражено как разность энтропии управляющей системы Н(Х) и условной энтропии управляющей системы после получения сообщения о состоянии управляемого объекта Н(Х/Y):
I(X,Y) = Н(Х) — Н(Х/Y). (2)
Подставив выражение (2) в правую часть выражения (1), получим
Н(Y)max — Н(Y/Х) = Н(Х) — Н(Х/Y). (3)
После переноса Н(Y)max из левой части выражения (3) в правую часть и замены знаков получим
Н(Y/Х)= Н(Y)max — Н(Х)+ Н(Х/Y). (4)
Выражение (4), определяющее предельные возможности управления, показывает, что для повышения качества управления, т.е. уменьшения энтропии Н(Y/Х), необходимо:
• уменьшать разнообразие состояний управляемого объекта Н(Y);
• увеличивать разнообразие управляющих воздействий Н(Х), приближая его к разнообразию состояний управляемого объекта Н(Y);
• уменьшать неоднозначность управляющих воздействий относительно состояний объекта управления Н(Х/Y), что возможно при наличии полной информации об управляемом объекте и внешней среде.
Иными словами, нужно стремиться к тому, чтобы на каждое возможное состояние управляемого объекта имелось свое управляющее воздействие, чтобы существовала возможность использования управляющих воздействий в зависимости от состояния и чтобы всякий раз обеспечивался выбор того воздействия, которое соответствует состоянию объекта управления.
Принцип Эшби. Выражение (4) отражает фундаментальный принцип кибернетики, известный как принцип необходимого разнообразия (принцип У. Росса Эшби) и формулируемый кратко так:
«Разнообразие управляющей системы должно быть не меньше разнообразия объекта управления».
Согласно данному принципу с увеличением сложности объекта управления сложность управляющей системы должна увеличиваться. При управлении нужно располагать возможно более точной и полной информацией об управляемом объекте и внешней среде.
Из этого принципа следует, что энтропию объекта управления (многообразие состояний регулируемых переменных) можно понизить до желаемого уровня (что и является целью регулирования), только увеличив энтропию управляющей системы (многообразие регулирующих переменных) по меньшей мере до соответствующего минимума.
Принцип утверждает также, что производительность любого физического устройства как регулятора не превышает его производительности как канала связи.
Проблемы установления критерия качества управления.
К сожалению, рассмотренная выше условная энтропия Н(Y/Х) не может считаться исчерпывающей характеристикой качества управления даже в теоретическом плане. дело в том, что значение энтропии зависит лишь от распределения вероятностей, но не от самих значений случайной величины. Между тем довольно часто более важны сами значения случайных отклонений, а не их вероятности. Кроме того, возможности управления ограничиваются и некоторыми другими факторами, например временем обработки информации в управляющем объекте и передачи ее по каналам прямой и обратной связи.
- << Назад
- Вперёд
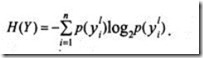
![clip_image018[4] clip_image018[4]](/images/stories/clip_image018-4_thumb.gif)
