Лекции для студентов

Лекция 5. Кручение. Кручение бруса некруглого сечения.

Расчет винтовых цилиндрических пружин с небольшим шагом 

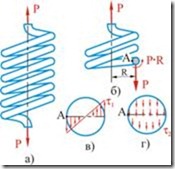
Пусть имеется винтовая цилиндрическая пружина с небольшим шагом витков, изготовленная из круглой проволоки и растягиваемая осевыми силами  (рис. 5.8). Вследствие малости шага витков будем считать, что плоскости отдельных витков пружины перпендикулярны к оси пружины. Рассечем виток пружины плоскостью, проходящей через ось пружины. Удалим одну часть пружины и рассмотрим равновесие оставшейся части (рис. 5.8, б). Для равновесия необходимо приложить в центре сечения силу , параллельную оси пружины и направленную вниз, и момент , где  — средний радиус витка пружины. Так как момент  действует в плоскости сечения, то он вызывает в сечении напряжения кручения (рис. 5.8, в), максимальная величина которых на внешних волокнах равна:

,                           (5.17)

где  - диаметр поперечного сечения проволоки.

Рис. 5.8 

Сила , действующая в плоскости поперечного сечения, вызывает в нем напряжение сдвига, которое будем считать равномерно распределенным по сечению (рис. 5.8, г). Это напряжение будет равно:

                                                    (5.18)

Для определения суммарных напряжений на внешних волокнах проволоки пружины следует сложить геометрически напряжения  и . Максимальное напряжение в сечении будет в той точке периферии сечения, в которой направления напряжений  и  совпадут. Нетрудно видеть, что такой точкой будет точка А. 

В этой точке напряжение будет равно:

         (5.19)

Мы рассмотрели растяжение пружины; совершенно такой же результат получился бы при рассмотрении сжатия пружины. При расчете пружин, у которых средний радиус пружины R во много раз больше диаметра d проволоки, из которой она изготовлена, вторым слагаемым, стоящим в скобках, обычно пренебрегают. Для таких пружин формула (5.19) упрощается и принимает вид 

                                               (5.20)

При расчете пружины, помимо расчета на прочность, часто необходимо бывает определить удлинение или сжатие (осадку) пружины, т. е. ее деформацию. Эта деформация, если принимать во внимание только кручение витков, будет определяться по формуле:

                                            (5.21)

где  - средний диаметр витка пружины;

 - число витков;