Лекции для студентов

Лекция 5. Кручение. Кручение бруса некруглого сечения.

Определение крутящего момента и построение эпюр крутящих моментов.

Для определения напряжений и деформаций произвольного вала необходимо знать величину крутящих моментов на его отдельных участках.

Крутящий момент  в произвольном сечении вала равен сумме внешних моментов , расположенных по одну сторону сечения.

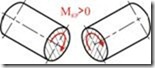
Крутящий момент  считается положительным, если при наблюдении с торца вдоль оси рассматриваемой части он стремится вращать сечение по часовой стрелке (рис. 5.6). 

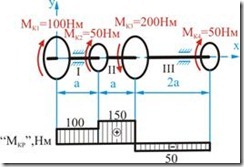
Рассмотрим в качестве примера построение эпюры крутящих моментов для трансмиссионного вала (рис. 5.7)

Рис. 5.6

Рис. 5.7

Разбиваем вал на участки , , .

Проведя произвольное сечение на первом участке:

, Н·м.

Для второго участка:

, Н·м.

На третьем участке рассматриваем правую часть от сечения, в котором определяем :

, Н·м.

Построенная эпюра показывает, что хотя к валу и приложен момент  Н·м, наибольший крутящий момент в сечении равен лишь  Н·м. Эту величину и следует использовать при расчете на прочность и жесткость.

На практике часто бывают заданы не моменты, приложенные к дискам (шкивам или зубчатым колесам), а передаваемые мощности , Вт, и частота вращения вала . Запишем зависимость между этими величинами.

В старой технической литературе использовалась единица мощности — лошадиная сила (1 л. с. ≈ 736 Вт). Если передаваемая мощность равна , л. с., то