Лекция 5. Кручение. Кручение бруса некруглого сечения.
Лекция 5. Кручение. Кручение бруса некруглого сечения.
Кручение прямого круглого бруса.
Деформация кручения вызывается парами сил, плоскости действия которых перпендикулярны к оси стержня. Поэтому при кручении в произвольном поперечном сечении стержня из шести внутренних силовых факторов возникает только один — крутящий момент ![]() . Как показывают опыты, поперечные сечения при кручении поворачиваются одно относительно другого вокруг оси стержня, при этом длина не меняется.
. Как показывают опыты, поперечные сечения при кручении поворачиваются одно относительно другого вокруг оси стержня, при этом длина не меняется.
Стержни, работающие на кручение, обычно называют валами.
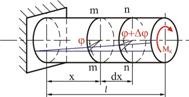
Рассматривая кручение вала, легко установить, что под действием скручивающего момента любое сечение на расстоянии ![]() от заделки поворачивается относительно закрепленного сечения на некоторый угол
от заделки поворачивается относительно закрепленного сечения на некоторый угол ![]() - угол закручивания (Рис. 5.1). При этом чем больше скручивающий момент
- угол закручивания (Рис. 5.1). При этом чем больше скручивающий момент ![]() , тем больше и угол закручивания. Зависимости
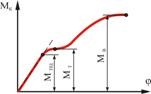
, тем больше и угол закручивания. Зависимости ![]() , называемые диаграммами кручения, полученные для образца из пластичного материала, до некоторой степени подобны диаграммам растяжения (Рис. 5.2). В дальнейшем при выводе формул для напряжений и угла закручивания нас будет интересовать участок диаграммы кручения, соответствующий работе материала в пределах пропорциональности.
, называемые диаграммами кручения, полученные для образца из пластичного материала, до некоторой степени подобны диаграммам растяжения (Рис. 5.2). В дальнейшем при выводе формул для напряжений и угла закручивания нас будет интересовать участок диаграммы кручения, соответствующий работе материала в пределах пропорциональности.
Рассмотрим геометрическую картину деформации вала при кручении.
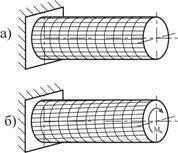
Если до деформации на поверхность вала нанести сетку, состоящую из линий, параллельных оси, и линий, представляющие собой параллельные круги, то после закручивания вала скручивающим моментом ![]() можно заметить следующее: образующие цилиндра превращаются в винтовые линии, параллельные круги не искривляются и расстояние между ними остается неизменным, радиусы, проведенные в торцевых сечениях остаются прямыми (Рис. 5.3). Полагая, что картина, наблюдаемая на поверхности вала, сохраняется и внутри, сформулируем гипотезы, взятые в основу теории кручения круглых стержней:
можно заметить следующее: образующие цилиндра превращаются в винтовые линии, параллельные круги не искривляются и расстояние между ними остается неизменным, радиусы, проведенные в торцевых сечениях остаются прямыми (Рис. 5.3). Полагая, что картина, наблюдаемая на поверхности вала, сохраняется и внутри, сформулируем гипотезы, взятые в основу теории кручения круглых стержней:
1. Поперечные сечения, плоские и нормальные к оси вала до деформации, остаются плоскими и нормальными к той же оси и после деформации.
На основании принятых гипотез кручение круглого вала можно представить как результат сдвигов, вызванных взаимным поворотом поперечных сечений относительно друг друга. Вследствие этого в поперечных сечениях возникают только касательные напряжения, а нормальные напряжения равны нулю.
Выделим из закручиваемого вала диск радиуса ![]() на расстоянии
на расстоянии ![]() от закрепленного конца, ограниченный двумя смежными сечениями
от закрепленного конца, ограниченный двумя смежными сечениями ![]() и
и ![]() , находящимися друг от друга на расстоянии
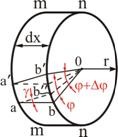
, находящимися друг от друга на расстоянии ![]() (Рис. 5.1) и рассмотрим его отдельно (Рис. 5.4)
(Рис. 5.1) и рассмотрим его отдельно (Рис. 5.4)
Проведем от точки ![]() прямую
прямую ![]() , параллельную
, параллельную![]() и соединим центр сечения
и соединим центр сечения ![]() с точкой
с точкой ![]() . Тогда угол
. Тогда угол ![]() , равный
, равный ![]() , будет углом поворота сечения
, будет углом поворота сечения ![]() относительно сечения
относительно сечения ![]() . У элемента
. У элемента ![]() до поворота сечения
до поворота сечения ![]() относительно сечения
относительно сечения ![]() верхняя и нижняя стороны были расположены горизонтально. После поворота стороны наклонились и приняли положение
верхняя и нижняя стороны были расположены горизонтально. После поворота стороны наклонились и приняли положение ![]() и
и ![]() . Следовательно, элемент претерпел абсолютный сдвиг, равный длине дуги:
. Следовательно, элемент претерпел абсолютный сдвиг, равный длине дуги:
Относительный сдвиг будет равен:
Отношение ![]() представляет относительный угол закручивания
представляет относительный угол закручивания ![]() (угол закручивания на единицу длины бруса). Тогда
(угол закручивания на единицу длины бруса). Тогда
Из этой формулы видно, что относительный сдвиг пропорционален радиусу закручиваемого цилиндрического тела.
На основании закона Гука для сдвига
Можно определить касательное напряжение для элементов лежащих на поверхности вала
Учитывая предположение, что деформация элементов на поверхности вала подобна деформации элементов внутри вала, для произвольного элемента, находящегося на расстоянии ![]() от центра поперечного сечения (рис 5.5)
от центра поперечного сечения (рис 5.5)
|
Рис. 5.5 |
Касательная элементарная сила на площадке Момент элементарной силы относительно оси бруса будет: |
Сумма таких элементарных моментов, распределенных по всему поперечному сечению ![]() , при равновесии, наступающем после деформации, должна быть равна крутящему моменту:
, при равновесии, наступающем после деформации, должна быть равна крутящему моменту:
Вынесем постоянные за знак интеграла, получим
Интеграл ![]() является полярным моментом инерции
является полярным моментом инерции ![]() (лекция 2, выражение (2.9)). Тогда
(лекция 2, выражение (2.9)). Тогда
Откуда относительный угол закручивания
Подставляя в выражение (5.5) выражение относительного угла закручивания получим
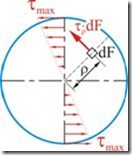
Это уравнение показывает, что напряжения в площадках сечения прямо пропорциональны их расстояниям до центра сечения.
При расчете на прочность при кручении необходимо знать максимальные напряжения для сравнения их с допускаемыми напряжениями. Очевидно, что максимальные напряжения при кручении круглого вала будут иметь точки максимально удаленные от оси вала. Т. е. точки с полярной координатой, равной радиусу сечения вала ![]()
Отношение полярного момента инерции![]() к наибольшему радиусу сечения
к наибольшему радиусу сечения ![]() называется полярным моментом сопротивления
называется полярным моментом сопротивления![]()
Тогда условие прочности при кручении будет иметь следующий вид
Для сплошного круглого сечения
Помимо расчета на прочность валы рассчитывают и на жесткость, ограничивая относительный угол закручивания некоторой допускаемой величиной ![]() :
: