Лекции для студентов

Лекция 3. Основы теории напряженного состояния.

Страница 3 из 4

Прямая задача в плоском напряженном состоянии. Круг напряжений (круг Мора).

Аналитическое решение прямой задачи дается формулами (3.2) — (3.5).

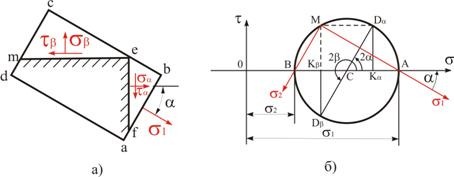
Проанализируем напряженное состояние, воспользовавшись простым графическим построением. Для этого введем в рассмотрение геометрическую плоскость и отнесем ее к прямоугольным координатным осям и . Порядок расчета опишем на примере напряженного состояния, изображенного на рис. 3.5, а.

Выбрав для напряжений некоторый масштаб, откладываем на оси абсцисс (рис 3.5, б) отрезки

На как на диаметре строим окружность с центром в точке . Построенный круг носит название круга напряжений или круга Мора.

Рис. 3.5

Координаты точек круга соответствуют нормальным и касательным напряжениям на различных площадках. Так, для определения напряжения на площадке, проведенной под углом (рис. 3.5, а) из центра круга (рис 3.5, б) проводим луч под углом до пересечения с окружностью в точке (положительные углы откладываем против часовой стрелки). Абсцисса точки (отрезок ) равна нормальному напряжению , а ордината ее (отрезок ) — касательному напряжению .

Напряжение на площадке, перпендикулярной к рассмотренной, найдем, проведя луч под углом и получив в пересечении с окружностью точку . Очевидно, ордината точки соответствует касательному напряжению , а абсцисса точки - нормальному напряжению .

Проведя из точки линию, параллельную (в нашем случае горизонталь), до пересечения с кругом, найдем полюс — точку . Линия, соединяющая полюс с любой точкой круга, параллельна направлению нормального напряжения на площадке, которой эта точка соответствует. Так, например, линия параллельна главному напряжению . Очевидно, что линия параллельна направлению главного напряжения .