Лекции для студентов

Лекция 3. Основы теории напряженного состояния.

Плоское напряженное состояние.

При исследовании напряженного состояния элементов конструкций наиболее часто приходится иметь дело с плоским напряженным состоянием. Оно встречается при кручении, изгибе и сложном сопротивлении. Поэтому на нем мы остановимся несколько подробнее.

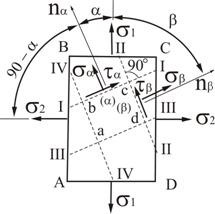
Рассмотрим элемент, грани которого являются главными площадками. 

Рис. 3.3

По ним действуют положительные напряжения  и , а третье главное напряжение  (направление  перпендикулярно к плоскости чертежа).

Проведем сечение I — I, которое определит площадку (), характеризуемую положительным углом . Напряжения  и  по этой площадке будут определяться по формулам:

                         (3.2)

                                          (3.3)

 

Сжимающие главные напряжения подставляют в эти формулы со знаком «минус», а угол  отсчитывают от алгебраически большего главного напряжения.

Проведем сечение II — II, которое определит площадку , перпендикулярную площадке . Нормаль  к ней образует с направлением  угол

.

Подставив в формулы (3.2) и (3.3) значения угла , будем иметь

;                       (3.4)

.                                     (3.5)

 

Совокупность формул (3.2) — (3.5) дает возможность находить напряжения по любым взаимно перпендикулярным наклонным площадкам, если известны главные напряжения.

Складывая равенства (3.2) и (3.4), обнаруживаем, что

,                                             (3.6)

 

т. е. сумма нормальных напряжений по двум взаимно перпендикулярным площадкам не зависит от угла наклона этих площадок и равна сумме главных напряжений.

Из формул (3.3) и (3.5) видим, что касательные напряжения достигают наибольшей величины при , т. е. по площадкам, наклоненным к главным площадкам под углом , причем

.                                                  (3.7)

 

Сравнивая формулы (3.3) и (3.5), находим, что

                                                       (3.8)

Это равенство выражает закон парности касательных напряжений.

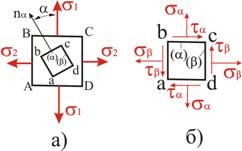
Проведем теперь еще два сечения (рис. 3.3): Сечение ІІІ — ІІІ, параллельное І — І, и сечение ІV – ІV, параллельное ІІ — ІІ. Элемент , выделенный четырьмя сечениями из элемента  (рис. 3.4, а), будет иметь вид, показанный на рис 3.4, б. Оба элемента определяют одно и то же напряженное состояние, но элемент  представляет его главными напряжениями, а элемент  - напряжениями на наклонных площадках.

Рис. 3.4

В теории напряженного состояния можно разграничить две основные задачи.

Прямая задача. В точке известны положения главных площадок и соответствующие им главные напряжения; требуется найти нормальные и касательные напряжения по площадкам, наклоненным под заданным углом  к главным.

Обратная задача. В точке известны нормальные и касательные напряжения, действующие в двух взаимно перпендикулярных площадках; требуется найти главные направления и главные напряжения. Обе задачи можно решать как аналитически, так и графически.