Лекция 2. Геометрические характеристики плоских сечений.
Наиболее практическое значение имеют главные центральные оси, центробежный момент инерции относительно которых равен нулю. Будем обозначать такие оси буквами ![]() и
и ![]() .
.
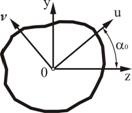
Чтобы определить положение главных центральных осей несимметричной фигуры, повернем произвольную начальную систему центральных осей ![]() ,
,![]() (рис 2.7) на некоторый угол
(рис 2.7) на некоторый угол ![]() при котором центробежный момент инерции становится равным нулю:
при котором центробежный момент инерции становится равным нулю:
Рис. 2.7
Согласно формулы (2.24)
откуда
Полученные из формулы (2.28) два значения угла ![]() отличаются друг от друга на 90° и дают положение главных осей. Как легко видеть, меньший из этих углов по абсолютной величине не превышает π/4. В дальнейшем будем пользоваться только меньшим углом. Проведенную под этим углом главную ось будем обозначать буквой
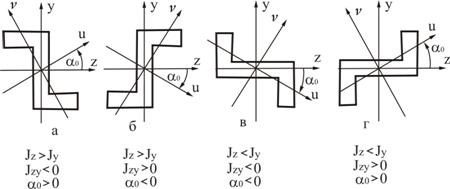
отличаются друг от друга на 90° и дают положение главных осей. Как легко видеть, меньший из этих углов по абсолютной величине не превышает π/4. В дальнейшем будем пользоваться только меньшим углом. Проведенную под этим углом главную ось будем обозначать буквой ![]() . На рис (2.8) приведены некоторые примеры обозначения главных осей в соответствии с указанным правилом. Начальные оси обозначаются буквами
. На рис (2.8) приведены некоторые примеры обозначения главных осей в соответствии с указанным правилом. Начальные оси обозначаются буквами ![]() и
и ![]() .
.
Рис. 2.8
Значения главных моментов инерции можно определить из следующих выражений:
Причем верхние знаки следует брать при ![]() >
>![]() , а нижние – при
, а нижние – при ![]() <
<![]() .
.