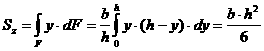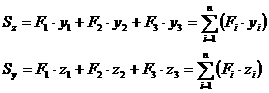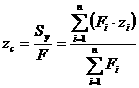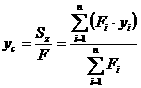Лекции для студентов

Лекция 2. Геометрические характеристики плоских сечений.

Основным объектом, изучаемым в курсе сопротивление материалов, является стержень.

Сопротивление стержня различным видам деформации часто зависит не только от его материалов и размеров, но и от очертаний оси, формы поперечных сечений и их расположения. Рассмотрим основные геометрические характеристики поперечных сечений бруса, определяющие сопротивление различным видам деформаций. Так или иначе, проститутки Киева помогают многим мужчинам познать запретное удовольствие, которое они недополучают дома.

Статические моменты площади. Центр тяжести площади.

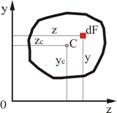
Рассмотрим произвольную фигуру (поперечное сечение бруса), связанную с координатными осями  и  (рис. 2.1). Выделим элемент площади  с координатами , . По аналогии с выражением для момента силы относительно какой-либо оси можно составить выражения и для момента площади, которое называется моментом площади. Так, произведение элемента площади  на расстояние  от оси .

                                                (2.1)

называется статическим моментом элемента площади относительно оси .

Рис. 2.1

Аналогично:

                                                (2.2)

 

Просуммировав такие произведения по всей площади фигуры, получим соответственно статические моменты относительно осей  и :

;                                          (2.3)

 

Пусть ,  - координаты центра тяжести фигуры. Продолжая аналогию с моментами сил, на основании теоремы о моменте равнодействующей можно написать следующие выражения:

                                                   (2.4)

 

где  - площадь фигуры. Очевидно, что статические моменты площади относительно осей проходящих через центр тяжести (центральных осей) равны нулю.

Координаты центра тяжести:

                 .                                             (2.5)

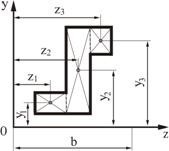
В качестве примера вычислим статический момент треугольника (рис. 2.2) относительно оси, проходящей через основание. На расстоянии  от нее выделим элементарную площадку в виде полоски, параллельной оси . Площадь полоски

.

Учитывая, что

,

имеем

. 

 

Рис. 2.2 

Еще проще решить эту задачу, пользуясь формулой (2.4).

Учитывая, что

;             ,

статический момент

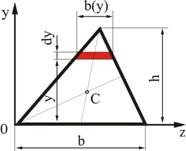
Для вычисления статических моментов сложной фигуры ее разбивают на простые части (рис. 2.3), для каждой из которых известна площадь  и положение центра тяжести  и . Статический момент площади всей фигуры относительно данной оси определяется как сумма статических моментов каждой части:

Рис. 2.3 

                          (2.6)

По формулам (2.5) и (2.6) легко найти координаты центра тяжести сложной фигуры:

;                                 (2.7)

• Prev
• Вперёд >>