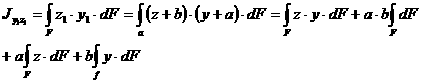Лекции для студентов

Лекция 2. Геометрические характеристики плоских сечений.

Моменты инерций сложных сечений, моменты инерций относительно параллельных осей

В расчетной практике часто приходится вычислять моменты инерции сложных сечений относительно различных осей, лежащих в плоскости фигуры. Для стандартных поперечных сечений стержней моменты инерции относительно различных осей даны в сортаменте.

При вычислении нестандартных сложных сечений последние можно разбить на отдельные простые части, моменты которых известны. Из основного свойства интеграла суммы следует, что момент инерции сложной фигуры равен сумме моментов инерции составных ее частей.

Если в сечении есть отверстие, его обычно удобно считать частью фигуры с отрицательной площадью. 

Моменты инерций относительно параллельных осей.

Пусть известны моменты инерции фигуры относительно центральных осей  и :

; ;                         (2.12)

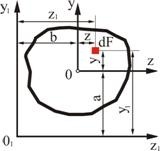
Требуется определить моменты инерции относительно осей, параллельных центральным (рис 2.5).

Рис. 2.5

; ; (2.13)

Координаты любой точки в новой системе  можно выразить через координаты в старых осях так:

;          

Подставим эти значения в формулы (2.13) и интегрируем почленно:

  (2.14)

    (2.15)

               (2.16)

Так как интегралы  и  равны нулю как статические моменты относительно центральных осей, то формулы (2.14) — (2.16) принимают вид

;

;                                                                                                   (2.17)

Зависимости между моментами инерции при повороте координатных осей.

Пусть известны моменты инерции произвольной фигуры (рис. 2. 6) относительно координатных осей ,:

; ;                         (2.18)

Повернем оси , на угол  против часовой стрелки, считая угол поворота осей в этом направлении положительным.

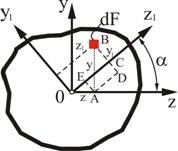
Рис. 2.6

Найдем теперь моменты инерции сечения относительно повернутых осей ,:

; ;                  (2.19)

Координаты произвольной элементарной площадки в новой системе  выражаются через координаты , прежней системы следующим образом:

                                     (2.20)

                                      (2.21)

Подставив эти выражения в (2.19) окончательно получим:

                                   (2.22)

                                   (2.23)

                                          (2.24)

Складывая почленно формулы (2.22),(2.23), находим

                                                  (2.25)

При повороте прямоугольных осей сумма моментов инерции не изменяется и равна полярному моменту инерции относительно начала координат.

• << Назад
• Вперёд >>