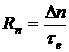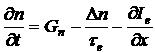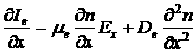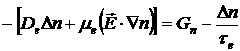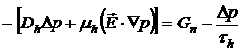Лекции для студентов

Физика полупроводников. Лекция 5

§6. Уравнение непрерывности для полупроводников.

Пусть в полупроводнике имеются неравновесные носители заряда, создаваемые под действием внешнего фактора. В результате процессов накопления и рассасывания концентрация неосновных носителей заряда в общем случае будет являться функцией координат и времени:

,

Поведение избыточных носителей заряда, концентрация которых зависит от координат и времени описывается с помощью уравнения непрерывности.

Представим себе одномерный полупроводник  — типа. Пусть вдоль оси x в нем создан положительный градиент концентрации электронов.

Пусть приложено внешнее электрическое поле. Положительный градиент концентрации можно создать с помощью омического контакта B. Выделим в полупроводнике слой толщиной dx,  — плотность тока электронов входящих в слой,  — плотность тока выходящих из слоя. Будем рассматривать полупроводник с площадью S = 1 см². Число электронов в слое в момент времени t будет равно , . Тогда изменение числа электронов за время dt будет равно:

(1)

Изменение числа электронов в слое dx может произойти за счет следующих процессов:

1. За счет генерации электронов в слое. При этом надо учитывать как тепловую генерацию, так и генерацию избыточных носителей заряда, за счет этих двух процессов , обеспечивает равновесную концентрацию ,  — скорость генерации избыточных электронов (неравновесных).

2. Изменение числа электронов за время dt в слое dx может быть связано с процессом рекомбинации электронов. Очевидно, за время dt в слое объемом dx будет рекомбинировано электронов:

(2)

,

3. Кроме того, из-за процесса диффузии электронов поток электронов входящих в слой dx может быть неравен потоку выходящего из слоя. Поток — это число электронов пересекающих в единицу времени единичную площадку.  — поток входящий в слой, а  — поток выходящий из слоя, следовательно за время dt изменение числа электронов в слое dx, за счет разности этих потоков будет равно:

(3)

Приравняем (1) с изменением числа электронов за счет перечисленных трех процессов.

(4)

Уравнение непрерывности для одномерного случая:

,

(5)

 — суммарная от внешнего поля и плюс поле объемного заряда,  — коэффициент диффузии электронов.

(6)

Подставим (6) в (4)

(7)

Если концентрация электронов является функцией координат и если все три компоненты электрического поля отличны от нуля, то уравнение непрерывности примет вид:

(8)

так как плотность дырочного тока равна

(9)

то уравнение непрерывности для дырок будет иметь вид:

(10)

В стационарных условиях уравнение непрерывности принимает вид:

(11)

(12)

(11), (12) — закон сохранения частиц. Согласно (11) поток электронов вытекающий из данного объема за единицу времени равен числу избыточных электронов генерируемых внешним фактором, за вычетом рекомбинируемых электронов.