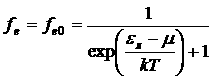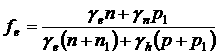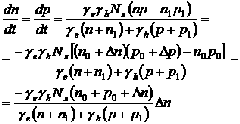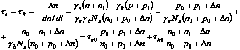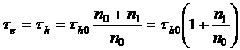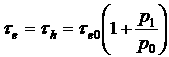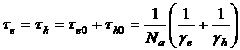Лекции для студентов

Физика полупроводников. Лекция 5

§3. Рекомбинация неравновесных носителей заряда на примесных центрах полупроводников.

Такая рекомбинация может быть основным механизмом в широкозонных полупроводниках при низких уровнях возбуждения. Рекомбинация на примесно-дефектных состояниях может быть ощутимой даже при концентрации примесей .

Будем рассматривать однозарядные рекомбинационные центры, т.е. такие которые могут быть в двух зарядовых состояниях: однозаряженном и нейтральном. Если это центры донорного типа, то они могут находиться в однократном положительном заряженном состоянии и нейтральном. Каждый рекомбинационный центр характеризуется двумя сечениями захвата: сечением захвата электронов и сечением захвата дырок .

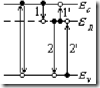
Дальше для определенности будем рассматривать примесно-рекомбинационные центры донорного типа. Начальным этапом рекомбинации в этом случае, очевидно, является захват электрона из зоны проводимости положительно заряженным донорным центром, а затем нейтрально заряженный центр захватывает дырку из валентной зоны (т.е. отдает электрон в валентную зону). В этом случае , потому что захват электрона происходит в притягивающем кулоновском поле. На рисунке показана схема рекомбинационных переходов через примесный уровень . Видно, что в результате электронных переходов 1 и 2 уничтожается электронно дырочная пара. Очевидно, время жизни электронно дырочной пары при такой рекомбинации при такой рекомбинации определяется в основном временем жизни неосновных носителей заряда (в данном случае дырок). Это связано с тем, что захваченный донором электрон находится достаточно долго на центре примеси пока не будет захвачена дырка (дырка захватывается медленнее, чем электрон). Эффективность рекомбинации неравновесных носителей заряда через примесные центры зависит от не только от вероятности захватами электронов и дырок, но и от вероятности обратных тепловых переходов 1', 2'.

Если у примесных центров вероятность обратных тепловых переходов значительна, то они называются центрами прилипания (это не рекомбинационные центры). Примесные центры, для которых вероятность обратных тепловых переходов незначительна, называются рекомбинационными центрами или ловушками. Найдем выражение для времени жизни неравновесных носителей заряда. Будем обозначать через  — концентрацию, а через:  — энергию ионизации рекомбинационных центров. Предположим, что в какой-то момент времени t = 0 включен источник внешнего возбуждения ( скорость генерации носителей заряда). С этого момента концентрация неравновесных электронов и дырок будет убывать до нуля. При этом скорость изменения концентрации электронов в зоне проводимости за единицу времени будет определяться двумя процессами: процессом рекомбинации электронов и процессом тепловой генерации электронов (то же самое относится к дыркам). Тогда скорость изменения концентрации в зоне проводимости будет следующая:

(1)

(2)

Первое слагаемое в (1) и (2) — рекомбинации, второе — тепло генерация.

 — коэффициенты рекомбинации электронов и дырок соответственно,  — коэффициенты тепловой генерации электронов и дырок соответственно,  — характеризует вероятность заполнения электронами примесных центров,  — вероятность заполнения дырками примесных центров. В равновесных условиях была бы функцией Ферми-Дирака.

,  — полная концентрация электронов и дырок. Найдем связь между коэффициентами рекомбинации и коэффициентами тепловой генерации. Так как равновесные и неравновесные электроны не различимы в зонах, то параметры и , а также и будут одинаковы как для равновесных, так и неравновесных электронов. В равновесном состоянии (только тепловые переходы):

,

Из (1) и (2), записанных в равновесном состоянии получаем:

(3)

(4)

(5)

Подставим (3), (4) в (1) и (2), получим:

(6)

(7)

Исходя из условия электронейтральности: , только незначительная часть электронов оседает на примесных центрах, тогда:

Значит в (6) и (7) левые части равны, следовательно, и правые равны. Из равенства находим выражение для функции распределения :

(8)

Подставим (8) в (6) или (7), получим:

(9)

Тогда время жизни неравновесных электронов и дырок будет равно:

(10)

 — время жизни электронов по отношению к их захвату ловушками, полностью заполненными дырками;  — время жизни дырок по отношению к их захвату ловушками, полностью заполненными электронами. (10) — формула Шотки — Холла — Рида. В ней первое слагаемое определяет время жизни электронов по отношению их захвата ловушками, а второе время жизни дырок по отношению их захвата ловушками.

Рассмотрим два предельных случая:

1. Низкий уровень возбуждения:

(11)

Видно, что в этом случае время жизни не зависит от условий возбуждения, т.е. от концентрации избыточных носителей заряда. Предположим, что при низких уровнях возбуждения исследуется монополярный полупроводник  — типа: , тогда из (11) следует

Для монополярного полупроводника  — типа:

Т.е. у таких полупроводников определяется временем жизни неосновных носителей заряда: дырок полупроводника  — типа, и электронов у полупроводника  — типа.

2. Высокий уровень возбуждения.

В этом случае время жизни носителей заряда не зависит от их концентрации, а зависит только от концентрации введенных ловушек и рекомбинационных параметров.