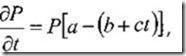Лекции для студентов

Курс лекций по “Общей экологии”. Часть 2

Моделирование

Моделирование. Под моделированием понимается изучение экологических процессов с помощью лабораторных, натурных или математических моделей. Модели биосистем многочисленны и классификация их почти невозможна.

Модель — это имитация того или иного явления реального мира, позволяющая делать прогнозы.

Модель может быть вербальной (словесной или графической), т. е. неформализованной. Если необходимы достаточно надежные количественные прогнозы, то модель должна быть формализованной, строго математической. Модели, созданные на ЭВМ, позволяют получать на выходе искомые характеристики при изменении, добавлении или исключении каких-либо параметров модели. Применение математики для отслеживания природных явлений используется для обработки экспериментов и описания работы биосистем становится. При этом необходимо доказать адекватность математического вида биосистемы реальному объекту.

Этапы в развития моделирования экосистем следующие:

1) переход от эксперимента к адекватной математической модели;

2) построение математических моделей с различной глубиной содержания;

3) переход от одних моделей к другим;

4) систематизация математических моделей биосистем различного уровня иерархии.

Но, несмотря на необходимость критического взгляда на математическое моделирование явлений природы обойтись только описательными методами уже невозможно. Стратегия моделирования заключается в попытке путем упрощения получить модель, свойства и поведение которой можно легко изучать. В то же время модель должна иметь достаточное сходство с оригиналом, чтобы результаты ее изучения были применимы к оригиналу. Переход от модели к оригиналу называется интерпретацией модели. Обычно оригинал представляет собой многокомпонентную систему, где взаимодействия между популяциями столь сложны, что не поддаются достаточно удовлетворительному анализу. В то же время законы функционирования некоторой модели могут быть найдены тем или иным путем. Учитывая это, исследования системы можно заменить исследованиями модели, о затем интерпретировать результаты применительно к оригиналу.

В 1980 г. была предложена следующая классификаций моделей, используемых в экологии (рис. 7.3).

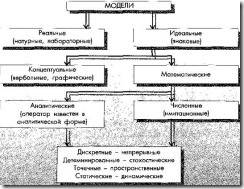
Рис 7. 3. Схема классификации моделей (по В. Д. Федорову и Т. Г. Гильманову .1980г.)

При работе с реальными лабораторными моделями установление адекватности модели оригиналу, а следовательно, обоснование возможности применения результатов моделирования к изучаемой природной системе. В отличие от аэро- или гидродинамики, где разработаны количественные критерии подобия модели оригиналу, в экологии таких критериев нет. Идеальные знаковые модели богаче возможностями, чем реальные, так как почти не связаны техническими ограничениями их создания. Знаковые модели — концептуальные и математические — имеют в экологии наибольшее значение.

Знаковые модели в экологии подразделяют на концептуальные и математические. Концептуальная модель — это в значительной степени формализованный вариант традиционного описания изучаемой экосистемы, состоящего из текста, блок-схемы, таблиц, графиков и иллюстративного материала. В итоговых публикациях Международной биологической программы (1964 — 1974) представлены концептуальные модели важнейших типов экосистем, обеспеченные количественными данными о динамике численности и биомассы популяций. Недостатки таких моделей — это неоднозначность интерпретаций и статичность.

Методы математического планирования при изучении динамики экосистем более эффективны. Математические модели классифицируют по признакам, в соответствии с которыми выбирается математический язык описания свойств, структуры и поведения экосистемы. Различают априорные (лат.- независимо от опыта) и апостериорные (лат.- основанные на опыте) модели. Априорные выводят на основании теоретических посылок, а апостериорные – на основании эмпирических данных. Выбор математического аппарата зависит также от состава фактической информации. Описания функционирования экосистем характеризуются неравномерностью изученности отдельных процессов. Кроме того, часто не известен как математический вид зависимостей между отдельными компонентами, так и какие-либо количественные характеристики процессов.

Попытки создания моделей, совмещающих физико-динамические и химико-биологические процессы, обычно приводят к использованию дифференциальных уравнений. Однако современное состояние некоторых математических дисциплин не позволяет достаточно подробно исследовать системы высокого порядка из-за нелинейностями связей между параметрами и факторами их определяющими. Это приводит к обобщению компонентов и характеристик для снижения порядка системы. Возможность получения модели, описывающей общие закономерности жизни экосистемы на основании аналитического исследования теоретических данных, была разработана Флемингом (1939) для роста биомассы микроскопических водорослей в водоеме (фитопланктона). Изменение биомассы в данной модели определяется двумя процессами: цветением водорослей и выеданием их микроскопическими животными (зоопланктоном).

Такая модель записывается в виде дифференциального уравнения первого порядка

(1)

где Р — биомасса фитопланктона а столбе воды над единицей площади;

a — удельная скорость роста биомассы фитопланктона; с — постоянный коэффициент увеличения скорости выедания фитопланктона зоопланктоном;

(b + ct)- коэффициент выедания, зависящий от времени t.

Численные значения коэффициентов уравнения были получены по материалам натурных исследований. Частное решение уравнения имеет вид

(2)

где Р₁ — биомасса в момент времени t;

Р_о -биомасса в момент времени t_о.

В период цветения такая зависимость эквивалентна увеличению биомассы зоопланктона, потребляющего определенную долю фитопланктона, выедаемого за сутки — DР.

Зависимость DР от количества зоопланктона N₁, и его фильтрационной способности V (л/сут) записывается в виде:

(3)

Из уравнений 1 и 3 получаем:

(4)

Общая биомасса фитопланктона С_t, за промежуток времени от t_o до t рассчитывается по уравнению (5):

(5)

Построение математической модели биосистемы можно выполнять параллельно с исследованием натуры или с постановкой лабораторных экспериментов. При этом поиск наилучшей структуры модели может производиться автоматически на ЭВМ на основании некоторой системы критериев. В этом случае на человека возлагаются выбор типа, структуры модели и критериев наилучшего сходства модели и оригинала, их изменение и смена.

Информационные потоки, состоящие из множества отдельных физических, химических и биологических показателей, не могут в полной мере отразить законы функционирования природного объекта. В связи с этим при моделировании экологических систем на основе дифференциальных уравнений следует использовать фундаментальные экологические принципы, в том числе принцип эмерджентности (экосистема обладает качественно новыми свойствами, которые нельзя предсказать исходя из свойств отдельных ее компонентов), т.к. необходимо учитывать, что экосистемы управляются и контролируются не всеми, а ключевыми, эмерджентными факторами. Поэтому для построения удовлетворительных математических моделей не требуется необъятного количества информации об огромном множестве переменных. Кроме того, стремление приблизиться к оригиналу с помощью наращивания показателей входит в противоречие с оперативностью решения задачи. Создание работоспособной модели многокомпонентной системы, функционирующей в трехмерном пространстве и во времени, связано с решением многих проблем, основными из которых являются следующие:

1. Выбор функциональных зависимостей и параметров, описывающих процессы обмена веществом и энергией между физическими и химико-биологическими компонентами.

2. Отсутствие пространственных наблюдений, т.е. ограниченный объем фактической информации, согласованных между собой физических, химических и биологических характеристик, изменяющихся во времени на начальном этапе моделирования приводит к несоответствию между желаниями исследователя и техническими возможностями. Операции заданий входной и анализа выходной информации перерастают в самостоятельные проблемы.

3. Реализация алгоритма моделирования экосистемы. Это связано с разработкой целого комплекса взаимосвязанных программ для описания весьма сложных физических и химико-биологических процессов. Решение каждой из задач в отдельности представляет собой самостоятельную проблему, требующую огромной работы. Далее возникает проблема информационной и программной увязки отдельных подсистем. Комплекс задач моделирования экосистемы в целом перерастает, по существу, в автоматизированную систему анализа поведения избранного объекта, а процесс создания Экологической» модели становится соизмеримым с процессом создания автоматизированных систем управления.