Лекции для студентов

Проектное управления: модели и методы принятия решений — Методы расчёта временных параметров и критического пути сетевой модели проекта

Методы расчета временных параметров и критического пути сетевой модели проекта

Если размеры сетевого графика невелики, то его временные параметры и критический путь могут быть найдены путем непосредственного рассмотрения графика вершина за вершиной, работа за работой. Но, естественно, по мере увеличения масштабов модели вероятность появления ошибки в расчетах будет возрастать в геометрической прогрессии. Поэтому, даже при небольших размерах модели целесообразно воспользоваться одним из наиболее подходящих алгоритмических методов расчета, позволяющих подойти к этой задаче формально.

Самыми распространенными методами расчета временных параметров сетевой модели являются табличный и матричный. Поэтому, даже если исходная информация по сетевой модели представлена в виде сетевого графика или временной диаграммы, приступая к анализу, ее следует привести к табличной либо матричной форме.

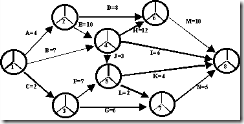
В качестве примера будем рассматривать модель, заданную изначально сетевым графиком, приведенным на рис. 6.

Рисунок 6. Пример сетевого графика для иллюстрации методов расчета временных параметров

Как табличный, так и матричный метод расчета временных параметров сетевой модели основывается на следующих соотношениях, вытекающих из определений временных параметров. Для удобства понимания индекс работы, как правило, состоит из двух букв, например, [ij], первая из которых соответствует индексу начального события работы, а вторая — индексу конечного события работы. С учетом этого замечания:

• Раннее время начала работы [ij] совпадает с ранним временем наступления события [i], т.е.
  ESTij = EET [i].
• Позднее время окончания работы [ij] совпадает с поздним временем наступления события [j], т.е.
  LFTij = LET [j].
• Раннее время окончания работы [ij]:

EFTij = ESTij + tij.

• Позднее время начала работы [ij]:
  LSTij = LFTij — tij.
• Раннее время наступления события [j] совпадает с самым поздним (максимальным) ранним временем окончания из всех тех работ, для которых данное событие является конечным, т.е.
  EET[j] = max { EFTrj, EFTnj, ..., EFTmj}, где [rj], [nj], ..., [mj] — индексы работ, для которых событие [j] является конечным.
• Позднее время наступления события [j] совпадает с самым ранним (минимальным) поздним временем начала из всех тех работ, для которых данное событие является начальным, т.е.
  LET[j] = min { LSTjr, LSTjn, ..., LSTjm}, где [jr], [jn], ..., [jm] — индексы работ, для которых событие [j] является начальным.
• Для исходного и заключительного события сетевой модели справедливо:
  EET[s] = LET[s]
• Но если для исходного события принимается, как правило, момент времени, равный 0, то для заключительного события он появляется в результате расчетов и по нему можно судить о продолжительности критического пути. Итак, для заключительного события справедливо:
  EET[f] = LET[f] = TK, где TK — продолжительность критического пути.
• Полный резерв времени выполнения работы [ij]:
  TFij = LЕT[j] — EET[i] — tij.
• Свободный резерв времени выполнения работы [ij]:
  FFij = EЕT[j] — EET[i] — tij.
• Независимый резерв времени выполнения работы [i]:
  IFi = EЕT[j] — LET[i] — tij.

Рассмотрим сначала матричный метод определения временных параметров.

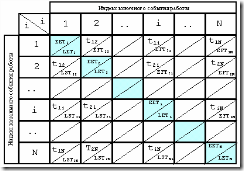
Прежде всего, необходимо составить квадратную матрицу (см. Рис. 7), число столбцов и строк, в которой равно числу событий сетевой модели. Строки и столбы индексируются в одинаковом порядке индексами события. Полученные на пересечении строк и столбцов клетки разбиваются на две части по диагонали снизу слева вверх вправо. Левая верхняя часть клетки называется ее числителем, правая нижняя — знаменателем.

Первый шаг заполнения матрицы заключается в следующем. Если события [i] и [j] соединяются какой-то работой, то продолжительность этой работы tij заносится в числители двух клеток: клетки, лежащей на пересечении i-й строки и j-го столбца, и клетки лежащей на пересечении j-й строки и i-го столбца. Эти действия выполняются для всех работ сетевой модели, а числители всех остальных клеток, кроме клеток, лежащих на главной (слева сверху вправо вниз) диагонали матрицы, заполняются нулями или вообще не заполняются.

Следующий шаг заполнения матрицы первоначально предполагает занесение в числитель первой клетки главной диагонали значения 0. Это равносильно тому, что мы полагаем, что раннее время наступления исходного события сетевой модели равно 0. Затем осуществляем заполнение знаменателей тех клеток первой строки, лежащих справа от (или над) главной диагонали, чьи числители содержат значения больше 0. При этом значения, которые проставляются в знаменатели, вычисляются как сумма числителя клетки данной строки, лежащей на главной диагонали, и числителя заполняемой клетки. Таким образом, мы подсчитываем раннее время окончания соответствующей работы. Результат выполнения этих действий приведен на рис. 8.

Рисунок 7. Разметка матрицы при определении временных параметров сетевой модели матричным методом

Рисунок 8.

Нетрудно проверить по формулам, что раннее время окончания работы 1-2 равно 4, а работы 1-4 равно 7.

Следующий шаг заполнения матрицы начинается с того, что мы должны решить, какое значение должно стоять в числителе диагональной клетки второй строки. По определению это должно быть значение, соответствующее раннему началу события 2. Раннее начало некоторого события, являющегося конечным для нескольких работ, равно моменту раннего окончания самой поздней из работ, которые заканчиваются данным событием. Значит, просто необходимо просмотреть знаменатели клеток столбца 2 сверху вниз до главной диагонали и выбрать максимальное значение, после чего записать его в числитель диагональной клетки 2. В нашем примере это будет знаменатель клетки 1-2, который равен 4.

После этого также, как были подсчитаны знаменатели в первой строке выше диагонали, подсчитываются знаменатели клеток второй строки выше диагонали.

Процедуры, описанные выше, повторяются до тех пор, пока не будет найден числитель последней диагональной клетки.

Дойдя до последней диагональной клетки (см. Рис. 9), мы получили значение раннего времени наступления завершающего события сетевой модели (36), которое и определяет продолжительность критического пути. Вместе с тем, для завершающего события, как известно, раннее время равно позднему времени его наступления, следовательно, знаменатель этой клетки будет равен ее числителю. Запишем это.

Рисунок 9

Получив значение знаменателя последней диагональной клетки, можно вычислить значения знаменателей клеток (чьи числители больше 0), находящихся в той же строке слева (ниже) от главной диагонали. Они будут равны разнице значения знаменателя соответствующей диагональной клетки и значения числителя клетки, для которой производится расчет. Так, например, значение знаменателя клетки 8-7 будет равно 36-5=31, а клетки 8-4 будет равно 36-6=30.

После подсчета всех знаменателей в последней строке можно найти значение знаменателя в диагональной клетке на предпоследней строке. Оно будет равно минимальному значению из знаменателей всех клеток, лежащих в данном столбце ниже главной диагонали, т.е. 31.

Затем аналогичным образом обсчитываем предпоследнюю строку и находим знаменатель третьей от конца диагональной клетки.

Из заполненной матрицы нетрудно увидеть не только продолжительность критического пути (числитель или знаменатель последней диагональной клетки), но также сам критический путь. Он проходит через события, у которых раннее и позднее время наступления равны, т.е. через события, у которых в соответствующих диагональных клетках совпадают числители и знаменатели. В нашем примере это будут события 1, 2, 4, 6, 8 (см. Рис. 9).

В соответствии с расчетными формулами резервов времени, которые были приведены выше, полный резерв времени выполнения работы, находящейся между событиями i и j, определяется разностью значений знаменателя диагональной клетки j-j и знаменателя клетки j в строке i выше главной диагонали. Чтобы найти свободный резерв времени выполнения работы, находящейся между событиями i и j, необходимо из числителя диагональной клетки j-j вычесть числитель диагональной клетки i-i и числитель клетки i-j. Чтобы найти независимый резерв времени выполнения работы, находящейся между событиями i и j, необходимо из числителя диагональной клетки j-j вычесть знаменатель диагональной клетки i-i и числитель клетки i-j.

Так, для работы 3-5 полный резерв будет равен 29-9=20, свободный — 17-2-7=8, а независимый — 17-22-7=-12 (принимается равным 0). Для работы 2-6 полный резерв будет равен 26-12=14, свободный — 26-4-8=14 и независимый — 26-4-8=14.

На рис. 10 приведены результаты расчетов всех резервов времени на основании данных из таблицы на рис. 9.

Табличный метод. Составляется таблица, число строк в которой равно числу работ, включающая в себя следующие столбцы (в порядке их следования слева направо):

1. индекс работы;
2. индексы непосредственно предшествующих работ;
3. индексы непосредственно следующих работ;
4. продолжительность выполнения работы;
5. раннее время начала выполнения работы;
6. позднее время начала выполнения работы;
7. раннее время окончания выполнения работы;
8. позднее время окончания выполнения работы;
9. полный резерв времени работы;
10. свободный резерв времени работы;
11. независимый резерв времени работы.

Исходная информация, связанная с описанием топологии сетевой модели, содержится в столбцах (1), (2) и (4). Суть табличного метода расчета временных параметров сетевой модели состоит в последовательном заполнении остальных столбцов данной таблицы.

Алгоритм табличного метода предусматривает выполнение следующих последовательных шагов.

Рисунок 10

ШАГ 1. Определение индексов непосредственно следующих работ.

Рассматриваем работу с индексом [i]. Непосредственно следующие за ней работы — это те работы, для которых работа [i] является непосредственно предшествующей. Следовательно, индексы непосредственно следующих работ — это индексы тех работ, у которых в столбце (2) содержится индекс работы [i].

ШАГ 2. Определение раннего времени начала и раннего времени окончания работ.

Определение раннего времени начала и раннего окончания работ, т.е. заполнение столбцов (5) и (7) таблицы должно осуществляться одновременно, т.к. время начала одних работ зависит от времени окончания других.

Заполнение указанных столбцов осуществляется последовательно от начала сетевой модели к ее концу, т.е. сверху вниз. При этом действуют следующие правила:

• Раннее время окончания рассматриваемой работы равно раннему времени ее начала (из столбца (5)) плюс продолжительность работы (из столбца (4)).
• Раннее время начала выполнения работы равно 0, если данной работе непосредственно не предшествует ни одна из работ сетевой модели, или равно максимальному раннему времени окончания среди всех непосредственно предшествующих ей работ (из столбца (7)).

Продолжительность критического пути равна максимальному значению в столбце (7).

ШАГ 3. Определение позднего времени окончания и позднего времени начала работ.

Определение позднего времени окончания и позднего начала работ, т.е. заполнение столбцов (6) и (8) таблицы должно осуществляться также одновременно, т.к. время начала одних работ зависит от времени окончания других.

Заполнение указанных столбцов осуществляется последовательно от конца сетевой модели к ее началу, т.е. снизу вверх. При этом действуют следующие правила:

• Позднее время начала рассматриваемой работы равно позднему времени ее окончания (из столбца (8)) минус продолжительность работы (из столбца (4)).
• Позднее время окончания выполнения работы равно продолжительности критического пути, если за данной работой нет ни одной непосредственно следующей работы (из столбца (3)) сетевой модели, или равно минимальному позднему времени начала среди всех непосредственно следующих за данной работой работ (из столбца (6)).

Шаг 4. Определение полного резерва времени выполнения работы.

Полный резерв времени работы [i] находится как разность значений ее позднего и раннего времени окончания (соответственно, столбцы (8) и (7)), либо как разность значений ее позднего и раннего начала выполнения (соответственно, столбцы (6) и (5)).

Шаг 5. Определение свободного резерва времени выполнения работы.

Свободный резерв времени работы [i] определяется как разность между значением раннего времени начала любой из непосредственно следующих за ней работ и суммой раннего времени начала работы [i] и ее продолжительности.

Шаг 6. Определение независимого резерва времени выполнения работы.

Независимый резерв времени работы [i] определяется как разность между значением раннего времени начала любой из непосредственно следующих за ней работ и суммой позднего времени наступления начального события работы [i] и ее продолжительности. Позднее время наступления начального события работы [i] табличным путем определяется как минимальное позднее время начала тех работ, у которых с работой [i] одинаковый состав непосредственно предшествующих работ.

По приведенным выше правилам заполнена следующая табл. 3.

Таблица 3.

Работа	Непосредс. Предшеств.	Непосредств Следующая.	t	EST	LST	EFT	LFT	TF	FF	IF
A	–	D, E	4	0	0	4	4	0	0	0
B	–	H, I, J	7	0	7	7	14	7	7	0
C	–	F, G	2	0	20	2	22	20	0	0
D	A	M	8	4	18	12	26	14	14	14
E	A	H, I, J	10	4	4	14	14	0	0	0
F	C	K, L	7	2	22	9	29	20	8	0
G	C	N	6	2	25	8	31	23	11	0
H	B, E	M	12	14	14	26	26	0	0	0
i	b, e	–	6	14	30	20	36	16	16	16
J	B, E	K, L	3	14	26	17	29	12	0	0
K	F, J	–	4	17	32	21	36	15	15	3
L	F, J	N	2	17	29	19	31	12	0	0
M	D, H	–	10	26	26	36	36	0	0	0
N	G, L	–	5	19	31	24	36	12	12	0