Лекции для студентов

Лекция 11. Статистическая неопределимость. Построение внутренних силовых факторов для плоских рам

Построение внутренних силовых факторов для плоских рам.

Рамами называют системы, состоящие из прямолинейных стержней, соединенных жесткими узлами.

Вертикально расположенные стержни рамы принято называть стойками, горизонтальные — ригелями.

Ось рамы представляет собой ломаную линию, однако каждый прямолинейный участок ее можно рассматривать как балку. Поэтому, чтобы построить какую либо эпюру для рамы, нужно построить ее для каждой отдельной балки, входящей в состав рамы. В отличие от обыкновенных балок в сечениях стержней рамы, кроме изгибающих моментов М и поперечных сил Q, обычно действуют еще и продольные силы N. Следовательно, для рам нужно строить эпюры , и .

Для и сохраняются ранее принятые правила знаков:

, если продольные силы вызывают растяжение;

, если ее векторы стремятся вращать части рассеченной рамы (относительно центра тяжести сечения) по часовой стрелке.

Для изгибающего момента специального правила знаков не устанавливают, а при установлении выражений для выбирают произвольно направление положительного момента.

Выражения для ,, и записывают очень редко — главным образом для тех участков, где действует распределенная нагрузка. Чаще всего просто вычисляют значения , и в характерных сечениях (на границах участков и в экстремальных точках), а затем проводят линии эпюр, учитывая особенности построения этих эпюр.

Ординаты эпюр, как и всегда, откладываем перпендикулярно к оси рамы, причем положительные ординаты и с внешней стороны рамы, а отрицательные — с внутренней (если, конечно, рама такой конфигурации, что можно различить ее наружную и внутреннюю стороны). Эпюры М условимся и для рам строить на сжатых волокнах.

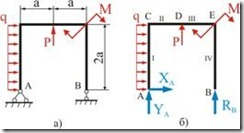
Рассмотрим пример построения эпюр внутренних силовых факторов для плоской рамы на рис. 2.4.4 a, нагруженной сосредоточенной парой , сосредоточенной силой и равномерно распределенной нагрузкой интенсивностью . Расстояние м.

Рис. 2.4.4

Так как рама имеет более одной опоры, то прежде чем приступить к построению эпюр, нужно найти опорные реакции (рис. 2.4.4 б).

; ; .

Эпюра «». Чтобы построить эпюру «», нужно спроецировать силы, приложенные к части рамы, лежащих по одну сторону от сечения, на ось стержня.

На участке : (растяжение).

На участке (рассматриваем правую часть):

На участке (рассматриваем правую часть):

На участке : (сжатие).

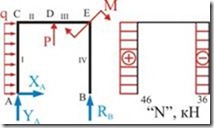
По этим данным строим эпюру «» (рис. 2.4.5)

Рис. 2.4.5

Эпюра «». В сечении стержня (т. е. в сечении , бесконечно близком к ) имеем

, кН.

В сечении стержня

Для любого сечения на участке сумма проекций лежащих справа сил на сечение одинакова и равна: , кН

Для любого сечения на участке сумма проекций лежащих справа сил на сечение одинакова, равна и дает отрицательную величину, т. к. сила стремится повернуть сечение на участке против часовой стрелки:

, кН.

Для любого сечения на участке сумма проекций нижележащих сил на сечение равна нулю:

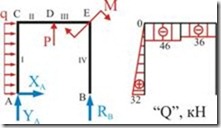
Эпюра «» представлена двумя прямоугольниками на ригеле рамы и треугольником на стойке (рис.2.4.6)

Рис. 2.4.6

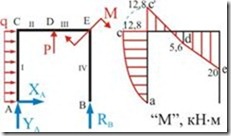
Эпюра «». Для построения эпюры «» будем вычислять величины изгибающих моментов в характерных сечениях , , . и .

Очевидно, что в точке : .

Очевидно и то, что в любом сечении стержня : .

В сечении стержня (т. е. в сечении , бесконечно близком к ) имеем

кН·м

Знак плюс в данном выражении мы выбирали, предполагая, что сжаты правые волокна. Получившийся знак минус при подстановке значения говорит о том, что в сечении стержня будут сжаты волокна слева. Поэтому на эпюре «» из точки откладываем влево координату, равную кН·м.

Поперечная сила на участке не меняет знак (не будет экстремальных значений на эпюре изгибающих моментов), поэтому для построения эпюры изгибающих моментов на данном участке проводим кривую второго порядка выпуклостью навстречу направлению распределенной нагрузки (выпуклостью влево). Учитывая, что поперечная сила в точке , касательная к эпюре моментов в этой точке параллельна оси участка (рис. 2.4.7).

В сечении стержня (в сечении , бесконечно близком к точке) изгибающий момент будет равен внешнему моменту :

кН·м.

Под действием момента сжимаются нижние волокна, поэтому значение кН·м будем откладывать вниз.

В сечении стержня (в сечении , бесконечно близком к точке) изгибающий момент будет равен

кН·м.

Положительный момент в сечении создавался внешним моментом , который сжимает нижние волокна. Поэтому положительное значение кН·м откладываем из точки вниз и проводим на эпюре «» прямую .

Так как в точке отсутствует внешний сосредоточенный момент, в сечении стержня имеем ту же величину изгибающего момента, что и для сечения стержня :

кН·м.

Рис. 2.4.7

В сечении стержня (т. е. в сечении , бесконечно близком к ), приняв, что положительный будет такой изгибающий момент, который вызывает сжатие нижних волокон, имеем такое же выражение момента, что и для сечения стержня

кН·м

Знак «минус» говорит о том, что в сечении стержня сжаты верхние волокна. Откладываем вверх координату, равную кН·м и проводим на эпюре изгибающих моментов прямую .