Лекции для студентов

Лекция 11. Статистическая неопределимость. Построение внутренних силовых факторов для плоских рам

Статическая неопределимость. Построение внутренних силовых факторов для плоских рам.

Статическая неопределимость.

С простыми статически неопределимыми системами мы уже сталкивались при расчете статически неопределимых стержней, работающими на чистое растяжение–сжатие.

Как уже указывалось, статически неопределимыми называются системы, силовые факторы в элементах которых только из уравнений равновесия определить нельзя. В таких системах связей больше, чем необходимо для равновесия.

Некоторые связи оказываются как бы лишними, а усилия в них — лишними неизвестными.

По числу лишних связей или лишних неизвестных усилий устанавливают степень статической неопределимости.

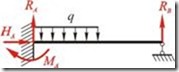
Рис.2.4.1

На рис.2.4.1 показана жестко закрепленная в точке А балка, опирающаяся в точке В на шарнирно-подвижную опору.

Из трех уравнений статики определить четыре реакции (, , , ) определить нельзя. Одна из реакций как бы получается лишней. В таком случае система является один раз статически неопределимая.

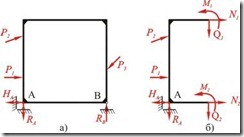
Статическая неопределимость может быть результатом не только наличием лишних связей, но также и условием образования системы. Рассмотрим раму, показанную на рис 2.4.2. Очевидно, что реакции , , внешних связей легко определить из уравнений равновесия. Однако после этого условия равновесия не позволяют определить все силовые факторы в ее элементах. Таким образом, из трех уравнений статики необходимо определить шесть неизвестных усилий. Следовательно, система является три раза статически неопределимой.

Для определения усилий в статически неопределимых системах дополнительно к уравнениям статики составляют уравнения совместности деформаций.

Рассмотрим этапы расчета статически неопределимой системы:

Рис. 2.4.2

1. Устанавливаем степень статической неопределимости (число лишних связей).

2. Удаляя лишние связи, заменяем исходную систему статически определимой, которая называется основной системой

3. Загружаем основную систему заданной нагрузкой и лишними неизвестными усилиями — такая система называется эквивалентной.

4. Приравниваем к нулю перемещения точек приложения неизвестных реакций по направлению их действия.

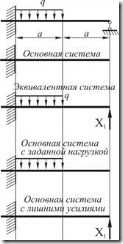
В качестве примера рассмотрим раскрытие статической неопределимости консольной балки (рис.2.4.3).

Защемление левого конца дает три реакции, шарнирно-подвижная опора — одну реакцию. Всего четыре реакции. Следовательно, балка один раз статически неопределимая. Для построения основной системы нужно устранить одну связь.

В качестве лишней связи выберем шарнирно-подвижную опору. Основная система, полученная в результате удаления лишней связи, представляет собой консоль.

Нагружаем основную систему заданной нагрузкой. Прогиб свободного конца балки по направлению неизвестной реакции

(2.4.1)

Рис. 2.4.3

Нагружаем основную систему неизвестной реакцией и определяем перемещение свободного конца балки от нагрузки в направлении ее действия. (2.4.2) Сумма перемещений должна равняться нулю (2.4.3) Откуда Зная одну неизвестную реакцию, из уравнений статики теперь легко можно определить неизвестные реакции.

Указанная схема расчета носит название метода сил, поскольку в качестве основных неизвестных здесь выбирают усилия лишних связей.

• Prev
• Вперёд >>