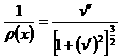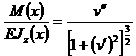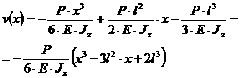Лекции для студентов

Лекция 7. Полный расчёт балок на прочность. Дифференциальное уравнение изогнутой оси

Дифференциальное уравнение изогнутой оси

Ранее были рассмотрены вопросы, относящиеся к расчету балок на прочность. В большинстве случаев практического расчета деталей, работающих на изгиб, необходимо также производить расчет их на жесткость.

Под расчетом на жесткость подразумевается оценка упругой податливости балки под действием приложенных нагрузок и подбор таких размеров поперечного сечения, при которых перемещения не будут превышать установленных нормами пределов.

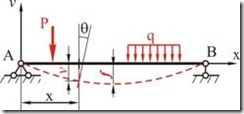
Рассмотрим деформацию балки при плоском изгибе (рис. 7.4). Ось балки под действием нагрузки, расположенной в одной из главных плоскостей инерции (плоскость ), искривляется в той же плоскости, а поперечные сечения поворачиваются и одновременно получают поступательное перемещение. Искривленная ось балки называется упругой линией.

Перемещение центра тяжести сечения по направлению, перпендикулярному к оси балки (), называется прогибом балки в данном сечении.

Рис. 7.4

Наибольший прогиб называется стрелой прогиба ().

Угол θ, на который каждое сечение поворачивается по отношению к своему первоначальному положению, называется углом поворота сечения.

Условимся, оси координат всегда располагать следующим образом: начало координат помещать на левом конце балки, ось направлять по оси балки вправо, а ось  — вверх.

Прогиб будем считать положительным, если перемещение соответствующей точки происходит вверх. Угол поворота будем считать положительным при повороте сечения против часовой стрелки.

Для определения прогибов балки воспользуемся уравнением, связывающим кривизну оси балки с изгибающим моментом и жесткостью сечения балки.

(7.1)

Из курса высшей математики известна следующая формула для кривизны линии

, (7.2)

где ; .

Подставляя (7.2) в (7.1) получим

(7.3)

Выражение (7.3) представляет точное дифференциальное уравнение изогнутой оси балки (упругой линии). Интегрирование данного уравнения представляет большие трудности. Однако для большинства практических задач величиной ввиду малости деформаций по сравнению с единицей можно пренебречь. Тогда получим упрощенное уравнение упругой линии:

(7.4)

В дальнейшем уравнение (7.4) будем называть основным дифференциальным уравнением упругой линии (для малых деформаций).

Решая задачу аналитическим способом, углы поворота и прогибы вычисляют последовательным интегрированием основного дифференциального уравнения (7.4). Проинтегрировав уравнение первый раз, получим выражение для угла поворота :

, (7.5)

содержащее одну произвольную постоянную . Интегрируя второй раз, находим выражение для погиба :

, (7.6)

содержащее две произвольные постоянные и .

Значения и определяют из условий закрепления балки. Так для балки.

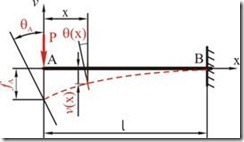
Пример. Определим максимальные значения прогиба и угла поворота сечения для консоли постоянного поперечного сечения с сосредоточенной силой на свободном конце.

Изгибающий момент в сечении будем вычислять как результат действия сил, расположенных справа от сечения:

.

Подставляя выражение для в уравнение (7.4), получаем

Интегрируем дважды:

.

Для определения постоянных и имеем граничные условия:

1) при ;

2) при ;

Рис. 7.5

Из второго условия

,

Откуда

Из первого условия

Откуда

Окончательные уравнения прогиба и угла поворота следующие:

Упругая линия представляет собой параболу третьей степени.

Легко убедиться, что и имеют место на свободном конце балки в точке (при) .

Отрицательное значение показывает, что прогиб происходит в направлении, противоположном направлению оси (т. е. вниз). Положительный угол поворота показывает, что поворот сечения происходит против часовой стрелки.

Сравнивая выражения и с выражениями для констант и , убеждаемся, что равно углу поворота крайнего левого сечения, а равно прогибу крайнего левого сечения консоли.