Лекции для студентов

Лекция 4. Теории прочности. Чистый сдвиг

Закон Гука при сдвиге.

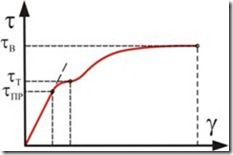
Для определения зависимости между нагрузкой и деформацией при сдвиге проводят испытания материала на кручение. При данном испытании строится диаграмма сдвига  (график зависимости между касательным напряжением и относительным сдвигом). Более подробное описание испытания на кручение образцов цилиндрической формы приведено в методических указаниях к лабораторным работам    

Для пластичных материалов диаграмма сдвига аналогична диаграмме растяжения (рис. 4.5).

Рис. 4.5

При рассмотрении деформации образца в пределах упругости видна линейная зависимость между относительным сдвигом  и касательным напряжением.

                                                        (4.24)

где  - коэффициент пропорциональности, который называется модулем упругости при сдвиге или модулем упругости второго рода.

Зависимость (4.24) выражает закон Гука при сдвиге.

Между величинами модуля продольной упругости  и модуля упругости при сдвиге  для одного и того же материала существует зависимость

                                                (4.25)

При значении коэффициента Пуассона  получим, что

Запишем выражение для перемещения одной грани относительно другой (абсолютного сдвига (рис. 4.1)) при чистом сдвиге. Обозначая площадь грани , равнодействующую сдвигающую силу  и расстояние между сдвигаемыми гранями  (рис. 4.1), получим

                                                   (4.26)

Формула (4.26) выражает закон Гука для абсолютного сдвига.