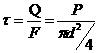Лекции для студентов

Лекция 4. Теории прочности. Чистый сдвиг

Страница 2 из 3

Сдвиг

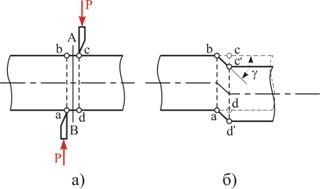
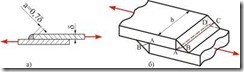
Если на брус действуют две равные силы , весьма близко расположенные друг к другу, перпендикулярные к оси бруса и направленные в противоположные стороны, как это бывает при разрезании прутков ножницами (рис. 4.1, а), то при достаточной величине сил происходит срез.

Рис. 4.1

Левая часть тела отделяется от правой по некоторому сечению . Деформация, предшествующая срезу, которая заключается в перекашивании прямых углов элементарного параллелепипеда, называется сдвигом. На рис. 4.1, б показан сдвиг, происходящий в параллелепипеде до среза; прямоугольник превращается в параллелограмм . Величина , на которую сечение сдвинулось относительно соседнего сечения , называется абсолютным сдвигом. Угол , на который изменяются прямые углы параллелепипеда, называется относительным сдвигом.

С учетом малости деформаций угол можно определить следующим образом:

(4.5)

Очевидно, что в сечении из шести внутренних силовых факторов будет возникать только поперечная сила , равная силе

(4.6)

Принимая, что касательные напряжения равномерно распределены по площади поперечного сечения , их значения можно определить по формуле

(4.7)

Допущение о равномерности распределения касательных напряжений по сечению весьма условно. Однако это допущение во многих случаях себя оправдывает и поэтому в инженерной практике им широко пользуются при расчете болтов, заклепочных соединений, шпонок, сварных соединений и других деталей.

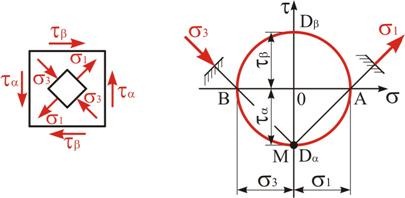
При расчете ряда элементов конструкций встречается частный случай плоского напряженного состояния, когда на четырех гранях прямоугольного элемента действуют только касательные напряжения (рис 4.2). Такое напряженное состояние называется чистым сдвигом.

Воспользуемся построением круга напряжений для определения величины и направления главных напряжений.

Рис. 4.2

Поскольку в данном случае

, а ,

находим, что главные площадки в данном случае наклонены к граням элемента под углом 45°, а главные напряжения равны

; ; . (4.8)

Проверим прочность элемента, испытывающего деформацию чистого сдвига.

Условие прочности составим по второй, третьей и четвертой теориям прочности:

а) по второй теории:

Подставляя значения главных напряжений, находим

(4.9)

Правая часть выражения представляет собой допускаемое напряжение при чистом сдвиге:

(4.10)

Для металлов . Следовательно, по второй теории прочности

; (4.11)

б) по третьей теории:

Подставляя значения главных напряжений, находим

. (4.12)

Т.е допускаемое напряжение при сдвиге по третьей теории

. (4.13)

б) по четвертой теории:

Подставляя значения главных напряжений, находим

. (4.14)

Следовательно, по четвертой теории прочности

(4.15)

Полученные величины допускаемых напряжений применяют также при расчетах на прочность деталей, испытывающих деформацию среза. Для пластичных материалов наиболее подходит формула (4.15). Например, для стали марки Ст3 допускаемое напряжение на растяжение и сжатие МПа. Тогда

.

Условие прочности на сдвиг (срез) может быть записано в обычном виде:

. (4.16)

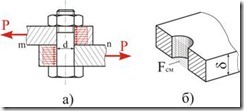
В качестве примера рассмотрим расчет болтового соединения, приведенного на рис. 4.3.

Рис. 4.3

Силы стремятся сдвинуть листы относительно друг друга. Этому препятствует болт, на который со стороны каждого листа передаются распределенные по контактной поверхности силы, равнодействующие которых равны . Усилия стремятся срезать болт в плоскости раздела листов , так как в этом сечении действует максимальная поперечная сила . Считая, что касательные напряжения распределены равномерно, получим

(4.17)

Таким образом, условие прочности болта на срез принимает вид

(4.18)

Отсюда можно найти диаметр болта:

(4.19)

При расчете болтовых, заклепочных и других соединений следует учитывать, что нагрузки, приложенные к элементам соединений, помимо среза вызывают смятие контактирующих поверхностей. Под смятием понимают пластическую деформацию, возникающую на поверхностях контакта

Максимальное напряжение смятия на цилиндрических поверхностях

,

где представляет собой площадь проекции поверхности контакта на диаметральную плоскость (рис.4.3)

(4.20)

Условие прочности на смятие имеет вид:

(4.21)

Допускаемые напряжения на смятие устанавливают опытным путем и принимают равным .

На основании зависимости (4.21) получим

(4.22)

Чтобы были удовлетворены условия прочности на срез и на смятие, из двух найденных диаметров следует взять больший, округлив его до стандартного значения.

На срез принято рассчитывать и некоторые сварные соединения.

Рис. 4.4

Если не учитывать наплывы, то в разрезе угловой шов имеет форму равнобедренного прямоугольного треугольника (рис. 4.4, а). Разрушение шва будет происходить по его минимальному сечению (рис. 4.4, б), высота которого