Лекции по метрологии. Часть 2: Виды и методы измерения
ВИДЫ И МЕТОДЫ ИЗМЕРЕНИЙ
Прежде чем разбираться в сущности каких-либо явлений, удобно их сначала упорядочить, т.е. классифицировать.
Измерения подразделяются на виды измерений — часть области измерений,
имеющая свои особенности и отличающаяся однородностью измеряемых величин, и методы измерений — часть области измерений, состоящая в различии приемов использования принципов и средств измерений.
Классификация видов измерений
Классификацию видов измерений можно проводить по различным классификационным признакам, к которым можно отнести следующие: способ нахождения численного значения физической величины, число наблюдений, характер зависимости измеряемой величины от времени, число измеряемых мгновенных значений в заданном интервале времени, условия, определяющие точность результатов, способ выражения результатов измерения (рис. 2.1) [7].
По способу нахождения численного значения физической величины измерения подразделяются на следующие виды: прямые, косвенные, совокупные и совместные.
Прямым измерением называют измерение, при котором значение измеряемой физической величины находят непосредственно из опытных данных. Прямые измерения характеризуются тем, что эксперимент как процесс измерения производится над самой измеряемом величиной, имея в виду то или
иное её проявление. Прямые измерения выполняются при помощи средств, предназначенных для измерения данных величин. Числовое значение измеряемой величины отсчитывается непосредственно по показанию измерительного прибора. средств, величин. Примеры прямых измерений: измерение тока амперметром; напряжения — компенсатором; массы — на рычажных весах и др.
Зависимость между измеряемой величиной X и результатом измерения Y при прямом измерении характеризуется уравнением X = Y, т.е. значение измеряемой величины принимается равным полученному результату.
К сожалению, прямое измерение не всегда можно провести. Иногда нет под рукой соответствующего измерительного прибора, или он неудовлетворяет.
| |
|
| |
 |
по точности, или даже вообще ещё не создан. В этом случае приходится прибегать к косвенному измерению.
Косвенными измерениями называют такие измерения, при которых значение искомой величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. При косвенных измерениях измеряют не собственно определяемую величину, а другие величины, функционально с ней связанные. Значение измеряемой косвенным путем величины X находят вычислением по формуле
X = F(Y1, Y2, … ,Yn),
где Y1 , Y2 , … Yn - значения величин, полученных путем прямых измерений.
Примером косвенного измерения является определение электрического сопротивления с помощью амперметра и вольтметра. Здесь путем прямых измерений находят значения падения напряжения U на сопротивлении R и ток I через него, а искомое сопротивление R находят по формуле
R = U/I .
Операцию вычисления измеряемой величины может производить вручную или с помощью вычислительного устройства, помещенного в прибор.
Прямые и косвенные измерения в настоящее время широко используются на практике и являются наиболее распространенными видами измерений .
Совокупные измерения — это производимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин.
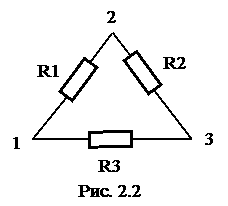
Например, для определения значений сопротивлений резисторов, соединенных треугольником (рис. 2.2), измеряют сопротивления на каждой
паре вершин треугольника и получают систему уравнений
![]()
![]() ;
;
![]() ;
;
![]() .
.
Из решения этой системы уравнений получают значения сопротивлений
![]() ,
, ![]() ,
, ![]() ,
,
где ![]() .
.
Совместные измерения — это производимые одновременно измерения двух или нескольких неодноименных величин X1, X2,…,Xn, значения которых находят решением системы уравнений:
Fi(X1, X2, … ,Xn; Yi1, Yi2, … ,Yim) = 0,
где i = 1, 2, …, m > n; Yi1, Yi2, … ,Yim — результаты прямых или косвенных измерений; X1, X2, … ,Xn — значения искомых величин.
Например, индуктивность катушки L = L0×(1 + w2×C×L0), где L0 — индуктивность при частоте w = 2×p×f , стремящейся к нулю; С — межвитковая емкость. Значения L0 и С нельзя найти прямыми или косвенными измерениями. Поэтому в простейшем случае измеряют L1 при w1 , а затем L2 при w2 и составляют систему уравнений:
![]() L1 = L0×(1 + w12×C×L0);
L1 = L0×(1 + w12×C×L0);
L2 = L0×(1 + w22×C×L0),
решая которую, находят искомые значения индуктивности L0 и емкости С:
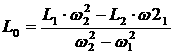 ;
; 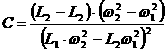 .
.
Совокупные и совместные измерения есть обобщение косвенных измерений на случай нескольких величин.
Для повышения точности совокупных и совместных измерений обеспечивают условие m ³ n, т.е. число уравнений должно быть больше или равно числу искомых величин. Получающуюся при этом несовместную систему уравнений решают методом наименьших квадратов.
По числу наблюдений измерения подразделяются на (рис.2.1):
- обыкновенные измерения — измерения, выполняемые с однократным наблюдением;
- статистические измерения — измерения с многократными наблюдениями.
Наблюдение при измерении — экспериментальная операция, выполняемая в процессе измерений, в результате которой получают одно значение из группы значений величин, подлежащих совместной обработке для получения результатов измерений.
Результат наблюдения — результат величины, получаемый при отдельном наблюдении.
По характеру зависимости измеряемой величины от времени измерения разделяются:
- на статические, при которых измеряемая величина остается постоянной во времени в процессе измерения;
- динамические, при которых измеряемая величина изменяется в процессе измерения и является непостоянной во времени.
При динамических измерениях для получения результата измерения необходимо учитывать это изменение. А для оценки точности результатов динамических измерений необходимо знание динамических свойств средств измерений [1].
По числу измеряемых мгновенных значений в заданном интервале времени измерения подразделяются на дискретные и непрерывные (аналоговые).
Дискретные измерения — измерения, при которых на заданном интервале времени число измеряемых мгновенных значений конечно.
Непрерывные (аналоговые) измерения — измерения, при которых на заданном интервале времени число измеряемых мгновенных значений бесконечно.
По условиям, определяющим точность результатов, измерения бывают:
- максимально возможной точности, достигаемой при существующем уровне техники;
- контрольно-поверочные, погрешность которых не должна превышать
некоторое заданное значение;
- технические, в которых погрешность результата определяется характеристиками средств измерений [11].
По способу выражения результатов измерения различают абсолютные и относительные измерения.
Абсолютные измерения — измерения, основанные на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.
Относительные измерения — измерения отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную [12].
- Prev
- Вперёд >>
