Лекции для студентов

Информационная безопасность. Лекция 8: Симметричные алгоритмы шифрования

Асимметричные алгоритмы шифрования

Алгоритмы шифрования с открытым ключом разрабатывались для того, чтобы решить две наиболее трудные задачи, возникшие при использовании симметричного шифрования.

Первой задачей является распределение ключа. При симметричном шифровании требуется, чтобы обе стороны уже имели общий ключ, который каким-то образом должен быть им заранее передан. Диффи, один из основоположников шифрования с открытым ключом, заметил, что это требование отрицает всю суть криптографии, а именно возможность поддерживать всеобщую секретность при коммуникациях.

Второй задачей является необходимость создания таких механизмов, при использовании которых невозможно было бы подменить кого-либо из участников, т.е. нужна цифровая подпись. При использовании коммуникаций для решения широкого круга задач, например в коммерческих и частных целях, электронные сообщения и документы должны иметь эквивалент подписи, содержащейся в бумажных документах. Необходимо создать метод, при использовании которого все участники будут убеждены, что электронное сообщение было послано конкретным участником. Это более сильное требование, чем аутентификация.

Диффи и Хеллман достигли значительных результатов, предложив способ решения обеих задач, который радикально отличается от всех предыдущих подходов к шифрованию.

Кроме этого, некоторые алгоритмы, например RSA, имеют следующую характеристику: каждый из двух ключей может использоваться как для шифрования, так и для дешифрования.

При описании симметричного шифрования и шифрования с открытым ключом будет использоваться следующая терминология. Ключ, используемый в симметричном шифровании, будет называться секретным ключом. Два ключа, используемые при шифровании с открытым ключом, будут называться открытым ключом и закрытым ключом. Закрытый ключ будет обозначаться KR, открытый ключ — KU.

Предполагается, что все участники имеют доступ к открытым ключам друг друга, а закрытые ключи создаются локально каждым участником и, следовательно, не распространяются. В любое время участник может изменить свой закрытый ключ и опубликовать составляющий пару открытый ключ, заменив им старый открытый ключ.

Диффи и Хеллман описывают требования, которым должен удовлетворять алгоритм шифрования с открытым ключом.

1. Вычислительно легко создавать пару (открытый ключ KU , закрытый ключ KR).
2. Вычислительно легко, имея открытый ключ и незашифрованное сообщение М, создать соответствующий зашифрованное сообщение:

С = ЕKU[М]

1. Вычислительно легко дешифровать сообщение, используя закрытый ключ:

М = DKR[C] = DKR[EKU[M]]

1. Вычислительно невозможно, зная открытый ключ KU, определить закрытый ключ KR.
2. Вычислительно невозможно, зная открытый ключ KU и зашифрованное сообщение С, восстановить исходное сообщение М.

Можно добавить шестое требование, хотя оно не выполняется для всех алгоритмов с открытым ключом:

1. Шифрующие и дешифрующие функции могут применяться в любом порядке:

М = ЕKU[DKR[M]]

Это достаточно сильные требования, которые вводят понятие односторонней функции с люком. Односторонней функцией называется такая функция, у которой каждый аргумент имеет единственное обратное значение, при этом вычислить саму функцию Y=f(X) легко, а вычислить обратную функцию X = f^-1(Y) — трудно (невозможно).

Односторонней функции с люком называется функция, которую, подобно односторонней функции, легко вычислить в одном направлении и трудно вычислить в обратном направлении до тех пор, пока недоступна некоторая дополнительная информация. При наличии этой дополнительной информации инверсию можно вычислить за приемлемое время.

Основные способы использования алгоритмов с открытым ключом

Основными способами использования алгоритмов с открытым ключом являются шифрование/дешифрование, создание и проверка подписи и обмен ключа.

Шифрование с открытым ключом состоит из следующих шагов:

1. Пользователь В создает пару ключей KU_b и KR_b, используемых для шифрования и дешифрования передаваемых сообщений.
2. Пользователь В делает доступным некоторым надежным способом свой ключ шифрования, т.е. открытый ключ KU_b. Составляющий пару закрытый ключ KR_b держится в секрете.
3. Если А хочет послать сообщение В, он шифрует сообщение, используя открытый ключ В KU_b .
4. Когда В получает сообщение, он дешифрует его, используя свой закрытый ключ KR_b. Никто другой не сможет дешифровать сообщение, так как этот закрытый ключ знает только В.

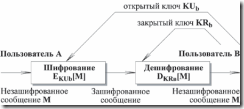
Рис.9.  Шифрование с открытым ключом

Создание и проверка подписи состоит из следующих шагов:

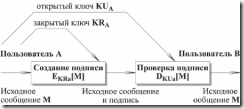
Рис.10.  Создание и проверка подписи

1. Пользователь А создает пару ключей KR_A и KU_A, используемых для создания и проверки подписи передаваемых сообщений.
2. Пользователь А делает доступным некоторым надежным способом свой ключ проверки, т.е. открытый ключ KU_A. Составляющий пару закрытый ключ KR_A держится в секрете.
3. Если А хочет послать подписанное сообщение В, он создает подпись E_KRa[M] для этого сообщения, используя свой закрытый ключ KR_A.
4. Когда В получает подписанное сообщение, он проверяет подпись D_KUa[M], используя открытый ключ А KU_A. Никто другой не может подписать сообщение, так как этот закрытый ключ знает только А.

Невозможно изменить сообщение, не имея доступа к закрытому ключу А, тем самым обеспечивается аутентификация и целостность данных.

В этой схеме все сообщение подписывается, причем для подтверждения целостности сообщения требуется много памяти. Каждое сообщение должно храниться в незашифрованном виде для использования в практических целях. Кроме того, копия сообщения также должна храниться в зашифрованном виде, чтобы можно было проверить в случае необходимости подпись. Более эффективным способом является шифрование небольшого блока битов, который является функцией от сообщения. Такой блок, называемый аутентификатором, должен обладать свойством невозможности изменения сообщения без изменения аутентификатора. Если аутентификатор зашифрован закрытым ключом отправителя, он является цифровой подписью, с помощью которой можно проверить исходное сообщение.

Важно подчеркнуть, что описанный процесс создания подписи не обеспечивает конфиденциальность. Это означает, что сообщение, посланное таким способом, невозможно изменить, но можно подсмотреть. Это очевидно в том случае, если подпись основана на аутентификаторе, так как само сообщение передается в явном виде. Но даже если осуществляется шифрование всего сообщения, конфиденциальность не обеспечивается, так как любой может расшифровать сообщение, используя открытый ключ отправителя.

Обмен ключей: две стороны взаимодействуют для обмена ключом сессии, который в дальнейшем можно использовать в алгоритме симметричного шифрования.

Некоторые алгоритмы можно задействовать тремя способами, в то время как другие могут использоваться одним или двумя способами.

Ниже приведены наиболее популярные алгоритмы с открытым ключом и возможные способы их применения.

Алгоритм	Шифрование / дешифрование	Цифровая подпись	Обмен ключей
RSA	Да; непригоден для больших блоков	Да	Да
DSS	Нет	Да	Нет
Диффи-Хеллман	Нет	Нет	Да