Лекции для студентов

Лекция 8. Определение перемещений при изгибе

Расчет балок переменного сечения на прочность и жесткость

До сих пор мы рассматривали расчет на изгиб стержней, сечение которых оставалось постоянным по длине. По конструктивным соображениям стержни, работающие на изгиб, часто имеют конусность, отверстия, выточки, ступеньки и т. д.

С точки зрения расчета на прочность и жесткость все такие стержни можно разделить на три основные группы:

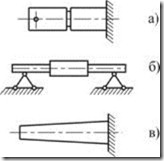
а) стержни, имеющие местные изменения формы и размеров сечений (рис. 2.1.3, а).

Рис. 2.1.3

б) стержни ступенчато-переменного сечения (Рис. 2.1.3, б);

в) стержни, имеющие непрерывно изменяющиеся по длине размеры сечений.

Разумеется, есть много деталей, в которых сочетаются различные виды нарушения размеров.

Перейдем к рассмотрению каждой группы в отдельности.

Местные изменения формы и размеров сечений вызывают резкое и значительное изменение картины распределения напряжений и деформаций. Однако это изменение носит местный характер и на напряженное состояние и деформированное состояние стержня в целом влияет незначительно.

Для высокопластичных материалов (малоуглеродистые стали, алюминий, медь) и хрупких неоднородных материалов (чугунов) концентрацию напряжений можно не учитывать и условие прочности запишется в обычном виде:

;

Для однородных хрупких материалов (высокопрочные закаленные стали)

,

где  — теоретический коэффициент концентрации, определяемый по справочным таблицам.

В обеих формулах  — это момент сопротивления ослабленного сечения.

Ступенчатые стержни будут иметь концентраторы напряжений в местах сопряжения участков с различными размерами поперечного сечения. При чувствительности материала к концентрации напряжений необходимо проверять условие прочности для соответствующих сечений с учетом коэффициента .

Для определения перемещений в ступенчатом стержне можно пользоваться видоизмененным методом начальных параметров. Рассмотрим на примере использование данного метода.

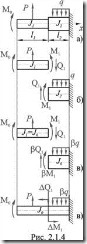
Балка на Рис. 2.1.4. имеет два участка постоянного поперечного сечения. Преобразуем заданную ступенчатую балку в эквивалентную балку постоянного сечения с моментом инерции , равным моменту инерции одного из участков балки, например первого.

Разрезаем балку в местах изменения размеров поперечного сечения и прикладываем в местах разрезов соответствующие внутренние силовые факторы — и .

Умножаем нагрузку на каждом участке на коэффициент приведения

Соединяем отдельные части, получаем эквивалентную балку постоянного сечения. Эта балка будет нагружена приведенными внешними нагрузками и дополнительными силами и моментами в местах сопряжения участков. Для определения перемещений в полученной эквивалентной балке можно использовать универсальное уравнение упругой линии.

Стержни с непрерывно меняющимися по длине размерами поперечного сечения при незначительном угле наклона образующей к оси стержня (до 15 — 20 °) рассчитывают с использованием обычного условия прочности

и дифференциального уравнения упругой линии

Расчет на прочность и жесткость осложняется тем, что момент сопротивления и момент инерции сечения являются функциями абсциссы сечения.

Частным случаем балок с непрерывно меняющимися по длине размерами являются балки равного сопротивления изгибу, во всех сечениях которого максимальное напряжение равно допускаемому

.

Отсюда получают уравнение для определения размеров балки равного сопротивления:

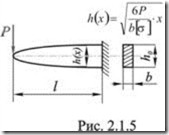
Для прямоугольного поперечного сечения с постоянной шириной сечения и переменной высотой сечения балка равного сопротивления показана на рис. 2.1.5.

Балка равного сопротивления параболического очертания наиболее рациональна с точки зрения экономии материала, однако из-за сложности формы не удовлетворяет техническим требованиям. Поэтому на практике применяют не балки равного сопротивления, а близкие к ним ступенчатые стержни.