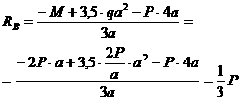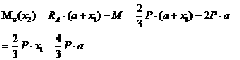Лекция 6. Чистый изгиб. Поперечный изгиб.
Как уже было сказано, при плоском поперечном изгибе в поперечном сечении балки возникают два внутренних силовых фактора ![]() и
и ![]() .
.
Перед определением ![]() и
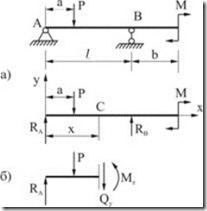
и ![]() определяют реакции опор балки (рис. 6.3, а), составляя уравнения равновесия статики.
определяют реакции опор балки (рис. 6.3, а), составляя уравнения равновесия статики.
Для определения ![]() и
и ![]() применим метод сечений. В интересующем нас месте сделаем мысленный разрез балки, например, на расстоянии
применим метод сечений. В интересующем нас месте сделаем мысленный разрез балки, например, на расстоянии ![]() от левой опоры. Отбросим одну из частей балки, например правую, и рассмотрим равновесие левой части (рис. 6.3, б). Взаимодействие частей балки заменим внутренними усилиями
от левой опоры. Отбросим одну из частей балки, например правую, и рассмотрим равновесие левой части (рис. 6.3, б). Взаимодействие частей балки заменим внутренними усилиями ![]() и
и ![]() .
.
Установим следующие правила знаков для ![]() и
и ![]() :
:
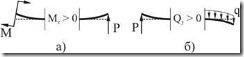
· Поперечная сила ![]() в сечении положительна, если ее векторы стремятся вращать рассматриваемое сечение по часовой стрелке;
в сечении положительна, если ее векторы стремятся вращать рассматриваемое сечение по часовой стрелке;
· Изгибающий момент ![]() в сечении положителен, если он вызывает сжатие верхних волокон.
в сечении положителен, если он вызывает сжатие верхних волокон.
Рис. 6.3
Для определения данных усилий используем два уравнения равновесия:
Таким образом,
а) поперечная сила ![]() в поперечном сечении балки численно равна алгебраической сумме проекций на поперечную ось сечения
в поперечном сечении балки численно равна алгебраической сумме проекций на поперечную ось сечения ![]() всех внешних сил, действующих по одну сторону от сечения;
всех внешних сил, действующих по одну сторону от сечения;
б) изгибающий момент в поперечном сечении балки численно равен алгебраической сумме моментов (вычисленных относительно центра тяжести сечения) внешних сил, действующих по одну сторону от данного сечения.
При практическом вычислении руководствуются обычно следующим:
1. Если внешняя нагрузка стремится повернуть балку относительно рассматриваемого сечения по часовой стрелке, (рис. 6.4, б) то в выражении для ![]() она дает положительное слагаемое.
она дает положительное слагаемое.
2. Если внешняя нагрузка создает относительно рассматриваемого сечения момент, вызывающий сжатие верхних волокон балки (рис. 6.4, а), то в выражении для ![]() в этом сечении она дает положительное слагаемое.
в этом сечении она дает положительное слагаемое.
Рис. 6.4
Построение эпюр ![clip_image102[9] clip_image102[9]](/images/stories/clip_image102-9_thumb_1.gif) и
и  в балках.
в балках.
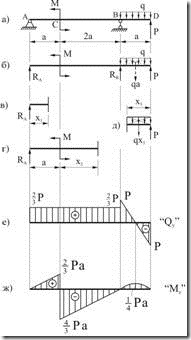
Рассмотрим двухопорную балку (рис. 6.5, а). На балку действует в точке ![]() сосредоточенный момент
сосредоточенный момент ![]() , в точке
, в точке ![]() - сосредоточенная сила
- сосредоточенная сила ![]() и на участке
и на участке ![]() - равномерно распределенная нагрузка интенсивностью
- равномерно распределенная нагрузка интенсивностью ![]() .
.
Определим опорные реакции ![]() и
и![]() (рис. 6.5, б). Равнодействующая распределенной нагрузки равна
(рис. 6.5, б). Равнодействующая распределенной нагрузки равна ![]() , а линия действия ее проходит через центр участка
, а линия действия ее проходит через центр участка ![]() . Составим уравнения моментов относительно точек
. Составим уравнения моментов относительно точек ![]() и
и ![]() .
.
Определим поперечную силу и изгибающий момент в произвольном сечений, расположенном на участке ![]() на расстоянии
на расстоянии ![]() от точки А (рис. 6.5, в). Расстояние
от точки А (рис. 6.5, в). Расстояние ![]() может изменяться в пределах (
может изменяться в пределах (![]() ).
).
Определим поперечную силу и изгибающий момент в произвольном сечений, расположенном на участке ![]() на расстоянии
на расстоянии ![]() от точки
от точки ![]() (рис. 6.5, г). Расстояние
(рис. 6.5, г). Расстояние ![]() может изменяться в пределах (
может изменяться в пределах (![]() ).
).
Значение поперечной силы не зависит от координаты сечения ![]() , следовательно, во всех сечениях участка
, следовательно, во всех сечениях участка ![]() поперечные силы одинаковы и эпюра
поперечные силы одинаковы и эпюра ![]() имеет вид прямоугольника. Изгибающий момент
имеет вид прямоугольника. Изгибающий момент
Изгибающий момент изменяется по линейному закону. Определим ординаты эпюры для границ участка.
Определим поперечную силу и изгибающий момент в произвольном сечений, расположенном на участке ![]() на расстоянии
на расстоянии ![]() от точки
от точки ![]() (рис. 6.5, д). Расстояние
(рис. 6.5, д). Расстояние ![]() может изменяться в пределах (
может изменяться в пределах (![]() ).
).
Поперечная сила изменяется по линейному закону. Определим для границ участка.
Изгибающий момент
Эпюра изгибающих моментов на этом участке будет параболической.
Чтобы определить экстремальное значение изгибающего момента, приравниваем к нулю производную от изгибающего момента по абсциссе сечения ![]() :
:
Отсюда
Для сечения с координатой ![]() значение изгибающего момента будет составлять
значение изгибающего момента будет составлять
В результате получаем эпюры поперечных сил (рис. 6.5, е) и изгибающих моментов (рис. 6.5, ж).
Дифференциальные зависимости при изгибе.
Эти зависимости позволяют установить некоторые особенности эпюр изгибающих моментов и поперечных сил:
1. На участках, где нет распределенной нагрузки, эпюры ![]() ограничены прямыми, параллельными нулевой линии эпюры, а эпюры
ограничены прямыми, параллельными нулевой линии эпюры, а эпюры ![]() в общем случае — наклонными прямыми.
в общем случае — наклонными прямыми.
2. На участках, где к балке приложена равномерно распределенная нагрузка ![]() , эпюра
, эпюра ![]() ограничена наклонными прямыми, а эпюра
ограничена наклонными прямыми, а эпюра ![]() - квадратичными параболами с выпуклостью, обращенной в сторону, противоположную направлению действия нагрузки
- квадратичными параболами с выпуклостью, обращенной в сторону, противоположную направлению действия нагрузки ![]() .
.
3. В сечениях, где ![]() , касательная к эпюре
, касательная к эпюре ![]() параллельна нулевой линии эпюры.
параллельна нулевой линии эпюры.
4. На участках, где ![]() , момент
, момент ![]() возрастает; на участках, где
возрастает; на участках, где ![]() , момент
, момент ![]() убывает.
убывает.
5. В сечениях, где к балке приложены сосредоточенные силы, на эпюре ![]() будут скачки на величину приложенных сил, а на эпюре
будут скачки на величину приложенных сил, а на эпюре ![]() будут переломы.
будут переломы.
6. В сечениях, где к балке приложены сосредоточенные моменты, на эпюре ![]() будут скачки на величину этих моментов.
будут скачки на величину этих моментов.
7. Ординаты эпюры ![]() пропорциональны тангенсу угла наклона касательной к эпюре
пропорциональны тангенсу угла наклона касательной к эпюре ![]() .
.
- << Назад
- Вперёд