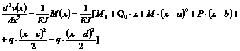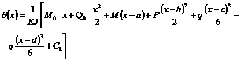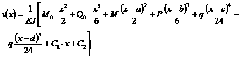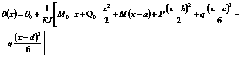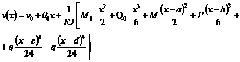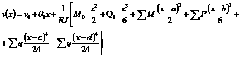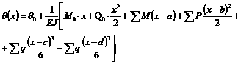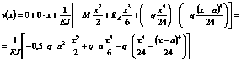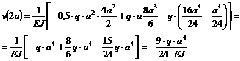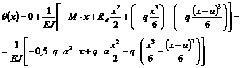Лекции для студентов

Лекция 8. Определение перемещений при изгибе

Определение перемещений при изгибе методом начальных параметров. Определение перемещений в балках переменного сечения

Определение перемещений при изгибе методом начальных параметров

Определение перемещений методом непосредственного интегрирования дифференциального уравнения упругой линии в случае балок с большим количеством участков сопряжено со значительными трудностями в определении большого количества постоянных интегрирования.

Для уменьшения большой вычислительной работы в настоящее время разработан ряд методик. К ним относится и метод начального интегрирования.

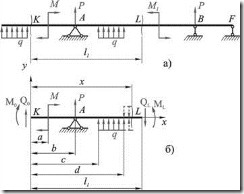
Рис. 2.1.1

Рассмотрим некоторую часть балки длиной (рис. 2.1.1,а), проведя сечения в точках и . На рис. 2.1.1,б изображен этот отрезок, нагруженный следующими наиболее часто встречающимися нагрузками:

а) сосредоточенным моментом М в сечении с абсциссой ;

б) сосредоточенной силой в сечении с абсциссой ;

в) равномерно распределенной нагрузкой от сечения с абсциссой до сечения с абсциссой .

г) кроме того, по концам рассматриваемой части балки приложены поперечные силы и изгибающие моменты, заменяющие действие мысленно отброшенных частей балки.

Начало координат выбираем в крайней левой точке рассматриваемой балки и делаем его общим для всех участков балки.

Возьмем произвольное сечение на расстоянии от начала координат.

При выводе уравнений направления всех нагрузок выбраны так, чтобы они вызывали положительные изгибающие моменты.

Выражения для изгибающих моментов будем составлять, рассматривая нагрузки слева от сечения с координатой . При включении в уравнения внешнего сосредоточенного момента умножим его на множитель , равный единице. В случае обрыва распределенной нагрузки ее продлевают до конца рассматриваемого сечения, а для восстановления действительных грузовых условий вводят «компенсирующую» нагрузку».

Интегрирование будем производить, не раскрывая скобок.

Составляем выражение изгибающего момента для сечения с координатой

Составим дифференциальное уравнение упругой линии

Интегрируем обе части равенства, не раскрывая скобок

Очевидно, что для

;

Следовательно, константы интегрирования и при подстановке начальных условий будут равны углу поворота и прогибу в начале координат. Прогиб и угол поворота являются начальными параметрами.

Для случая нескольких моментов и сил, а также нескольких участков распределенной нагрузки уравнение записывают в следующей форме:

Данное уравнение обычно называют универсальным уравнением упругой линии.

Дифференцируя универсальное уравнение прогибов, получаем уравнение углов поворота сечений

В универсальные уравнения подставляются только те нагрузки, которые расположены слева от рассматриваемого сечения. Началом координат принимается крайнее левое сечение балки.

Таким образом, определение перемещений по методу начальных параметров сводится в первую очередь к определению величин начальных параметров и , которые определяются из условий закрепления балки.

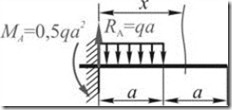
Определим прогиб и угол поворота сечения свободного конца консольной балки, нагруженной распределенной нагрузкой (Рис. 2.1.2).

Рис. 2.1.2

В защемлении при заданной нагрузке будет возникать реакция и реакционный момент .

Очевидно, что при данном виде закрепления

;

Подставляем нагрузки в универсальные уравнения.

Для

Для