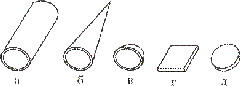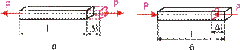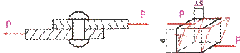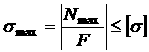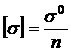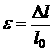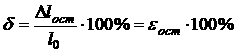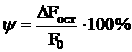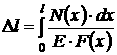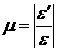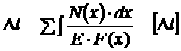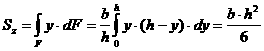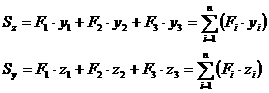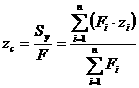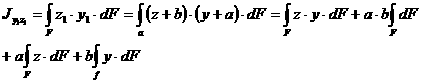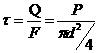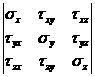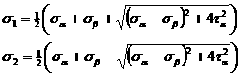Сопромат
Лекция 1. Задачи и метод сопротивления материалов. Растяжение и сжатие.
1. Лекция . Задачи и методы сопротивления материалов. Растяжение и сжатие.{jcomments on}
Общие понятия.
Возведение сооружений и строительство машин (которые далее будем называть конструкциями) начинается с составления проекта, в котором определяют форму, размеры и материал конструкции. Каждая конструкция составляется из отдельных деталей, взаимно соединенных между собой. Эти детали будем называть элементами конструкций. В процессе эксплуатации элементы в той или иной степени участвуют в работе и подвергаются действию различных внешних факторов: нагрузок, изменений температуры.
Под влиянием внешних сил элементы конструкций изменяют свою первоначальную геометрическую форму, объем и размеры. Такое изменение называют деформацией.
Величина деформации может при определенных условиях нарушить нормальную работу конструкции и даже оказаться опасной для целости того или иного элемента.
Для обеспечения нормальной и безопасной работы конструкция должна удовлетворять условиям прочности, жесткости и надежности.
Прочность – это способность конструкции выдерживать заданную нагрузку, не разрушаясь.
Жесткость — способность конструкции под действием внешних сил сопротивляться возникновению деформации.
Надежность — свойство конструкции выполнять заданные функции, сохраняя свои эксплуатационные показатели в определенных нормативных пределах в течение требуемого промежутка времени.
Этими вопросами и занимается наука сопротивление материалов.
Сопротивление материалов — наука, в которой изложены принципы и методы расчета элементов конструкций на прочность, жесткость и надежность.
Кроме этих требований, проектируемые сооружения должны удовлетворять требованиям наибольшей экономичности и долговечности.
Основные формы элементов конструкций
При всем разнообразии видов элементов конструкций их можно свести к сравнительно небольшому числу основных форм.
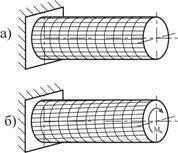
Стержень или брус — тело, у которого один размер (длина) значительно превышает два других (поперечных) размера (рис. 1).
В машиностроении встречаются стержни как прямолинейные (рис. 1, а), так и криволинейные (рис. 1, б), как постоянного (рис. 1, а), так и переменного (рис. 1, в) сечения.
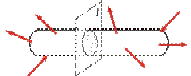
Стержни, у которых толщина стенки значительно меньше габаритных размеров поперечного сечения, называют тонкостенными (рис. 1, г). В настоящее время они широко применяются в строительных конструкциях, судо- и особенно в авиастроении.
Рис. 1
Оболочка представляет собой тело, ограниченное криволинейными поверхностями, расположенными на близком расстоянии друг от друга.
Поверхность, которая делит толщину оболочки на равные части, называется срединной. По форме срединной поверхности различают оболочки цилиндрические (рис. 2, а), конические (рис. 2, б), сферические (рис. 2, в) и др. К оболочкам относятся неплоские стенки тонкостенных резервуаров, котлов, купола зданий, обшивки фюзеляжа, крыла и других частей летательных аппаратов, корпуса подводных лодок и т. д.
Если срединная поверхность представляет собой плоскость, то расчетный объект называют пластинкой (рис. 2, г). Встречаются пластинки круглые (рис. 2, д), прямоугольные (рис. 2, г) и других очертаний. К пластинкам могут быть отнесены плоские днища и крышки резервуаров, перекрытия инженерных сооружений, диски турбомашин и т. п.
Рис. 2
Тела, у которых все три размера одного порядка, называют массивными телами. К ним относятся фундаменты сооружений, подпорные стенки и т. п.
Основные виды деформаций.
Как уже говорилось, под действием нагрузок конструкция деформируется, т. е. форма и размеры ее могут изменяться.
Деформации бывают упругие, т. е. исчезающие после прекращения действия вызвавших их сил, и пластические, или остаточные, — не исчезающие.
Деформации элементов конструкций могут быть очень сложными, но эти сложные деформации всегда можно представить состоящими из небольшого числа основных видов деформаций.
Основными видами деформаций элементов конструкций являются:
1. растяжение (рис. 3, а) или сжатие (рис. 3, б). Растяжение или сжатие возникает, например, в случае, когда к стержню по его оси приложены противоположно направленные силы.
Рис. 3
Изменение ![]() первоначальной длины
первоначальной длины ![]() стержня называют абсолютным удлинением при растяжении и абсолютным укорочением при сжатии. Отношение абсолютного удлинения (укорочения)
стержня называют абсолютным удлинением при растяжении и абсолютным укорочением при сжатии. Отношение абсолютного удлинения (укорочения) ![]() к первоначальной длине стержня
к первоначальной длине стержня ![]() называют относительным удлинением на длине
называют относительным удлинением на длине ![]() и обозначают
и обозначают ![]()
2. сдвиг или срез (рис. 4). Сдвиг или срез возникает, когда внешние силы смещают два параллельных плоских сечения стержня одно относительно другого при неизменном расстоянии между ними;
Рис. 4
Величина смещения ![]() называется абсолютным сдвигом. Отношение абсолютного сдвига к расстоянию
называется абсолютным сдвигом. Отношение абсолютного сдвига к расстоянию ![]() между смещающимися плоскостями называют относительным сдвигом. Вследствие малости угла
между смещающимися плоскостями называют относительным сдвигом. Вследствие малости угла ![]() при упругих деформациях его тангенс принимают равным углу перекоса рассматриваемого элемента. Следовательно, относительный сдвиг
при упругих деформациях его тангенс принимают равным углу перекоса рассматриваемого элемента. Следовательно, относительный сдвиг
3. кручение (рис. 5). Кручение возникает при действии на стержень внешних сил, образующих момент относительно оси стержня;
4.
Рис. 5
Деформация кручения сопровождается поворотом поперечных сечений стержня относительно друг друга вокруг его оси. Угол поворота одного сечения стержня относительно другого, находящегося на расстоянии ![]() , называют углом закручивания на длине
, называют углом закручивания на длине ![]() . Отношение угла закручивания
. Отношение угла закручивания ![]() к длине
к длине ![]() называют относительным углом закручивания:
называют относительным углом закручивания:
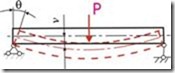
6. изгиб (рис. 6). Деформация изгиба заключается в искривлении оси прямого стержня или в изменении кривизны кривого стержня.
Рис. 6
В прямых стержнях перемещения точек, направленные перпендикулярно к начальному расположению оси, называют прогибами и обозначают буквой ![]() . При изгибе происходит также поворот сечений стержня вокруг осей, лежащих в плоскостях сечений. Углы поворота сечений относительно их первоначальных положений обозначают буквой
. При изгибе происходит также поворот сечений стержня вокруг осей, лежащих в плоскостях сечений. Углы поворота сечений относительно их первоначальных положений обозначают буквой ![]() .
.
Основные гипотезы науки о сопротивлении материалов.
Для построения теории сопротивления материалов принимают некоторые допущения (гипотезы) относительно структуры и свойств материалов, а также о характере деформации.
7. Гипотеза о сплошности материала. Предполагается, что материал сплошь заполняет форму тела. Атомическая теория дискретного состояния вещества во внимание не принимается.
8. Гипотеза об однородности и изотропности. В любом объеме и в любом направлении свойства материала считаются одинаковыми. В некоторых случаях предположение об изотропии неприемлемо. Например, свойства древесины вдоль и поперек волокон существенно различны.
9. Гипотеза о малости деформации. Предполагается, что деформации малы по сравнению с размерами тела. Это позволяет составлять уравнения статики для недеформированного тела.
10. Гипотеза об идеальной упругости материала. Все тела предполагаются абсолютно упругими.
Перечисленные выше гипотезы намного упрощают решение задач по расчету на прочность, жесткость и устойчивость. Результаты расчетов хорошо сходятся с данными практики.
Внутренние силы. Метод сечений.
Внутри любого материала имеются внутренние междуатомные силы, наличие которых определяет способность тела воспринимать действующие на него внешние силы, сопротивляться разрушению, изменению формы и размеров. Приложение к телу внешней нагрузки вызывает изменение внутренних сил. В сопротивлении материалов изучаются дополнительные внутренние силы. В сопротивлении материалов они называются просто внутренними силами.
Внутренние силы — силы взаимодействия между отдельными элементами конструкций или между отдельными частями элемента, возникающие под действием внешних сил.
Чтобы численно установить величину внутренних сил пользуются методом сечений.
Метод сечений сводится к четырем действиям:
1. Разрезают (мысленно) тело плоскостью ![]() в том месте, где нужно определить внутренние силы (рис. 7);
в том месте, где нужно определить внутренние силы (рис. 7);
Рис. 7
2. Отбрасывают любую отрезанную часть тела (желательно наиболее сложную), а ее действие на оставшуюся часть заменяют внутренними силами, чтобы оставшаяся исследуемая часть находилась в равновесии (рис.8);
Рис. 8
3. Приводят систему сил к одной точке (как правило, к центру тяжести сечения) и проецируют главный вектор и главный момент системы внутренних сил на нормаль к плоскости (ось ![]() ) и главные центральные оси сечения (
) и главные центральные оси сечения (![]() и
и ![]() ).
).
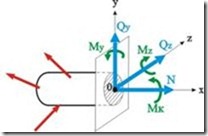
Полученные силы (N, Qy, Qz) (рис. 9) и моменты (Мк, Мy, Mz) называют внутренними силовыми факторами в сечении
Рис. 9
Для внутренних силовых факторов приняты следующие названия:
4. Находят внутренние силовые факторы, составляя шесть уравнений равновесия статики для рассматриваемой части рассеченного тела.
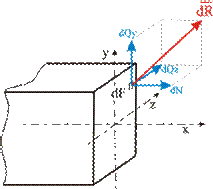
Если в сечении выделить бесконечно малую площадку ![]() и предположить, что внутренние силы, приложенные к его различным точкам, одинаковы по величине и направлению, то равнодействующая их
и предположить, что внутренние силы, приложенные к его различным точкам, одинаковы по величине и направлению, то равнодействующая их ![]() будет проходить через центр тяжести элемента
будет проходить через центр тяжести элемента ![]() (рис. 10).
(рис. 10).
Рис. 10
Проекциями ![]() на оси
на оси ![]() ,
,![]() и
и ![]() будут элементарная продольная сила
будут элементарная продольная сила ![]() , и элементарные поперечные силы
, и элементарные поперечные силы ![]() и
и ![]() .
.
Разделим эти элементарные силы на площадь ![]() , получим величины, называемые напряжениями в точке проведенного сечения.
, получим величины, называемые напряжениями в точке проведенного сечения.
где ![]() — нормальное напряжение;
— нормальное напряжение; ![]() — касательное напряжение.
— касательное напряжение.
Напряжение — внутренняя сила, отнесенная к единице площади в данной точке рассматриваемого сечения.
Напряжение измеряется в единицах напряжения — паскалях (Па) и кратных ему — (кПа, МПа)
Иногда кроме нормальных и касательных напряжений рассматривают еще и полное напряжение
Понятие «напряжение» играет очень важную роль в расчетах на прочность. Поэтому значительная часть курса сопротивления материалов отводится изучению способов вычисления напряжений ![]() и
и ![]() .
.
Растяжение и сжатие
Центральным растяжением (сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила (растягивающая и сжимающая) а все остальные внутренние силовые факторы равны нулю.
Растягивающие продольные силы принято считать положительными, а сжимающие — отрицательными.
Продольные силы определяются с помощью метода сечений.
Пример
Пусть имеется ступенчатый стержень, нагруженный силами ![]() ,
, ![]() и
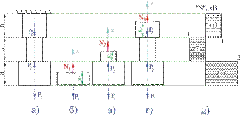
и ![]() вдоль оси стержня, показанного на рис. 11, а. Определить величину продольных сил.
вдоль оси стержня, показанного на рис. 11, а. Определить величину продольных сил.
Решение. Стержень может быть разделен на участки по местам приложения нагрузок и по местам изменения поперечного сечения.
Первый участок ограничен точками приложения сил ![]() и
и ![]() . Направим ось
. Направим ось ![]() вдоль оси участка вверх с началом координат в точке приложения силы
вдоль оси участка вверх с началом координат в точке приложения силы ![]() (начало первого участка). Мысленно рассечем первый участок поперечным сечением на расстоянии
(начало первого участка). Мысленно рассечем первый участок поперечным сечением на расстоянии ![]() от начала первого участка. Причем координата
от начала первого участка. Причем координата ![]() может быть взята в интервале
может быть взята в интервале ![]() , где
, где ![]() — длина первого участка.
— длина первого участка.
Рассмотрим равновесие нижней части стержня, заменив действие верхней части на нижнюю часть стержня продольной силой ![]() , предварительно направив ее в сторону растяжения рассматриваемой части.
, предварительно направив ее в сторону растяжения рассматриваемой части.
Из условия равновесия статики:
Положительный знак продольной силы говорит о том, что первый участок растянут.
Значение продольной силы не зависит от координаты ![]() , поэтому на всем участке значение продольной силы постоянно и равно
, поэтому на всем участке значение продольной силы постоянно и равно ![]() .
.
Рис. 11
Второй участок ограничен точками приложения сил ![]() и
и ![]() . Направим ось
. Направим ось ![]() вдоль оси участка вверх с началом координат в точке приложения силы
вдоль оси участка вверх с началом координат в точке приложения силы ![]() (начало второго участка).
(начало второго участка).
Мысленно рассечем второй участок поперечным сечением на расстоянии ![]() от начала второго участка. Причем координата
от начала второго участка. Причем координата ![]() может быть взята в интервале
может быть взята в интервале ![]() , где
, где ![]() — длина второго участка.
— длина второго участка.
Рассмотрим равновесие нижней части стержня, заменив действие верхней части на нижнюю часть стержня продольной силой ![]() , предварительно направив ее в сторону растяжения рассматриваемой части.
, предварительно направив ее в сторону растяжения рассматриваемой части.
Из условия равновесия статики:
Знак минус говорит о том, что второй участок сжат.
Аналогично для третьего участка :
Полученные результаты для большей наглядности удобней представить в виде графика (эпюры N), показывающего изменение продольной силы вдоль оси стержня. Для этого проводим нулевую (базовую) линию параллельно оси стержня, перпендикулярно которой будем в масштабе откладывать значения осевых усилий (рис. 1.11, д). В одну сторону откладываем положительные значения, в другую — отрицательные. Эпюра заштриховывается перпендикулярно нулевой линии, а в нутрии эпюры ставится знак откладываемой величины. Рядом указываются значения откладываемых величин. Рядом с эпюрой в кавычках указывается название эпюры («N») и через запятую — единицы измерения (кН)
Нормальные напряжения
Отсутствие поперечных сил при растяжении (сжатии) дает основание предположить, что в каждой точке поперечного сечения касательные напряжения равны нулю.
Продольная сила в сечении бруса является равнодействующей нормальных напряжений, действующих в плоскости поперечного сечения.
Закон распределения напряжений может быть определен из эксперимента. Установлено, что если на стержень нанести прямоугольную сетку, то после приложения продольной нагрузки вид сетки не изменится, она по-прежнему останется прямоугольной, а все линии прямыми. Поэтому можно сделать вывод о равномерном по сечению распределении продольных деформаций и перейти к гипотезе плоских сечений.
Гипотеза плоских сечений: поперечные сечения стержня, плоские и нормальные к его оси до деформации остаются плоскими и нормальными к оси и при деформации.
Так как одинаковым удлинениям соответствуют одинаковые напряжения, то напряжения ![]() всех волокон в поперечном сечении будут одинаковы. Тогда
всех волокон в поперечном сечении будут одинаковы. Тогда
откуда
Отметим, что полученное выражение справедливо для сечений достаточно удаленных от мест приложения сосредоточенных нагрузок. Вблизи приложения нагрузок распределение напряжений носит сложный характер.
Для обеспечения прочности стержня должно выполняться условие прочности — конструкция будет прочной, если максимальное напряжение ![]() ни в одной точке нагруженной конструкции не превышает допускаемой величины
ни в одной точке нагруженной конструкции не превышает допускаемой величины![]() , определяемой свойствами данного материала и условиями работы конструкции, то есть
, определяемой свойствами данного материала и условиями работы конструкции, то есть
Допускаемое напряжение
![]() — коэффициент запаса прочности. Величина коэффициента запаса прочности назначается в пределах
— коэффициент запаса прочности. Величина коэффициента запаса прочности назначается в пределах ![]() , а иногда и более, с учетом многих факторов, в частности, точности принятых расчетных соотношений, условий эксплуатации конструкции, особых требований по безопасности работы, норм, принятых в отрасли промышленности. В машинах и аппаратах химических производств
, а иногда и более, с учетом многих факторов, в частности, точности принятых расчетных соотношений, условий эксплуатации конструкции, особых требований по безопасности работы, норм, принятых в отрасли промышленности. В машинах и аппаратах химических производств ![]() .
.
Испытания механических свойств материалов
Для определения опасных напряжений ![]() необходимо провести испытания образцов материала на растяжение и сжатие (более подробно эта тема рассмотрена в методических указаниях к лабораторным работам по сопротивлению материалов (1 часть)»
необходимо провести испытания образцов материала на растяжение и сжатие (более подробно эта тема рассмотрена в методических указаниях к лабораторным работам по сопротивлению материалов (1 часть)»
Испытания материалов на растяжение (сжатие) заключается в построении кривых зависимостей между величиной удлинения ![]() (укорочения) и величиной силы
(укорочения) и величиной силы ![]() , которая вызвала данное удлинение (укорочение). От диаграммы растяжения в координатах
, которая вызвала данное удлинение (укорочение). От диаграммы растяжения в координатах ![]() и
и ![]() можно, разделив все ординаты на площадь поперечного сечения образца
можно, разделив все ординаты на площадь поперечного сечения образца ![]() , а абсциссы на первоначальную длину образца
, а абсциссы на первоначальную длину образца ![]() , перейти к диаграмме в координатах
, перейти к диаграмме в координатах ![]() и
и ![]() , где:
, где:
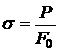 — нормальное напряжение в поперечном сечении образца;
— нормальное напряжение в поперечном сечении образца;
Диаграмма ![]() —
— ![]() более удобна и лучше отражает физические свойства материала, так как она не зависит от геометрических размеров испытываемого образца.
более удобна и лучше отражает физические свойства материала, так как она не зависит от геометрических размеров испытываемого образца.
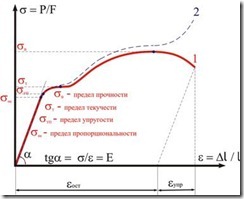
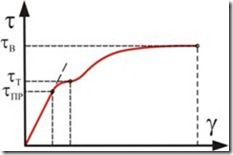
Рассмотрим характерные точки диаграммы ![]() —
— ![]() растяжения малоуглеродистой стали (рис. 12, кривая 1), которые характеризуют прочность исследуемого материала. Данная диаграмма называется диаграммой условных напряжений, так как напряжения определяются отношением силы на первоначальную площадь поперечного сечения.
растяжения малоуглеродистой стали (рис. 12, кривая 1), которые характеризуют прочность исследуемого материала. Данная диаграмма называется диаграммой условных напряжений, так как напряжения определяются отношением силы на первоначальную площадь поперечного сечения.
Диаграмма истинных напряжений (рис. 12, кривая 2) в диапазоне напряжений, соответствующих характеристикам прочности, мало отличается от диаграммы условных напряжений, поэтому на практике используют диаграммы условных напряжений.
Рис. 12 Диаграммы растяжения в координатах ![]() —
— ![]() .
.
До определенного значения напряжения имеет место линейная зависимость между величинами относительного удлинения ![]() и напряжения
и напряжения ![]() . Материал в данном случае подчиняется закону Гука — закону пропорциональности нагрузки и деформации.
. Материал в данном случае подчиняется закону Гука — закону пропорциональности нагрузки и деформации.
где коэффициент пропорциональности ![]() — модуль продольной упругости(модуль Юнга), величина которого постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки..
— модуль продольной упругости(модуль Юнга), величина которого постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки..
Максимальное напряжение ![]() , до которого материал подчиняется закону Гука, называется пределом пропорциональности.
, до которого материал подчиняется закону Гука, называется пределом пропорциональности.
Выше предела пропорциональности наблюдается нелинейная зависимость напряжения от относительной деформации.
До какого то значения напряжения после снятия нагрузки материал все еще не имеет остаточных деформаций.
Наибольшее напряжение ![]() , до которого остаточная деформация при разгрузке не обнаруживается, называется пределом упругости.
, до которого остаточная деформация при разгрузке не обнаруживается, называется пределом упругости.
Предел упругости является характеристикой, не связанной с законом Гука. Предел упругости может иметь значение как выше, так и ниже значения предела пропорциональности. Эти напряжения близки друг к другу и обычно различием между ними пренебрегают.
При каком то значении напряжения удлинение образца растет при практически постоянном значении растягивающей силы. Такой процесс деформации называется текучестью материала.
Наименьшее напряжение ![]() , при котором деформация образца происходит при постоянном растягивающем усилии, называется пределом текучести.
, при котором деформация образца происходит при постоянном растягивающем усилии, называется пределом текучести.
Для металлов, не имеющих площадки текучести, предел текучести определяют условно как напряжение, при котором остаточная деформация составляет 0,2 %.
После стадии текучести материал вновь приобретает способность увеличивать сопротивление дальнейшей деформации.
Напряжение, соответствующее максимальной нагрузке ![]() , которую может воспринимать образец, называется пределом прочности или временным сопротивлением.
, которую может воспринимать образец, называется пределом прочности или временным сопротивлением.
После достижения максимального усилия при дальнейшем растяжении образца деформация происходит, главным образом, на небольшой длине образца. Это ведет к образованию местного сужения в виде шейки и к падению силы (рис. 12. кривая 1), несмотря на то, что истинное напряжение в сечении шейки непрерывно растет (рис. 12. кривая 2).
Полное удлинение, полученное образцом перед разрушением, уменьшится после разрыва, так как в частях образца исчезнут упругие деформации.
Отношение в процентах приращения расчетной длины образца ![]() после разрыва к его первоначальной длине
после разрыва к его первоначальной длине ![]() , называется относительным остаточным удлинением
, называется относительным остаточным удлинением ![]() :
:
Отношение в процентах абсолютного уменьшения площади поперечного сечения в шейке ![]() к первоначальной площади
к первоначальной площади ![]() , называется относительным остаточным сужением.
, называется относительным остаточным сужением.![]() :
:
Относительное остаточное удлинение и относительное остаточное сужение являются характеристиками пластичности материала.
Испытание на сжатие, несмотря на простоту, проводят реже, так как модуль упругости ![]() , предел упругости и предел текучести при сжатии примерно те же, что и при растяжении.
, предел упругости и предел текучести при сжатии примерно те же, что и при растяжении.
Испытанию на сжатие подвергают главным образом хрупкие материалы, которые, как правило, лучше сопротивляются сжатию, чем растяжению, и применяются для изготовления элементов, работающих на сжатие.
Подробное описание испытания на сжатие описано в методических указаниях к лабораторным работам по дисциплине «Сопротивление материалов» (первая часть).
Деформации при растяжении (сжатии)
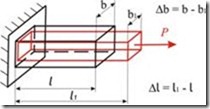
При растяжении стержня постоянного поперечного сечения длина увеличивается, а поперечные размеры уменьшаются (рис. 13).
Рис. 13
Из закона Гука
Если на рассматриваемом участке продольная сила и поперечное сечение переменны, то удлинение участка длиной ![]() получим, суммируя удлинения бесконечно малых участков.
получим, суммируя удлинения бесконечно малых участков.
где ![]() — координата бесконечно малого участка;
— координата бесконечно малого участка;
![]() — продольная сила в сечении с координатой
— продольная сила в сечении с координатой ![]() ;
;
![]() — длина бесконечно малого участка;
— длина бесконечно малого участка;
![]() — площадь поперечного сечения стержня с координатой
— площадь поперечного сечения стержня с координатой ![]() .
.
Если мы возьмем произвольный поперечный размер ![]() , то его изменение, отнесенное к его первоначальному значению, даст нам относительную поперечную деформацию (рис. 13):
, то его изменение, отнесенное к его первоначальному значению, даст нам относительную поперечную деформацию (рис. 13):
Между поперечной и продольной относительной деформацией при простом растяжении (сжатии) в пределах применимости закона Гука существует постоянное отношение. Абсолютная величина этого отношения носит название Коэффициента Пуассона и обозначается буквой ![]() :
:
Учитывая, что продольная и поперечная деформация всегда имеют противоположные знаки, получаем
Коэффициент Пуассона наряду с модулем продольной упругости характеризует упругие свойства материалов.
В некоторых случаях для обеспечения нормальной работы конструкций размеры их элементов нужно выбирать так, чтобы обеспечивалось условие жесткости. При растяжении (сжатии) условие жесткости имеет следующий вид:
где ![]() — изменение размеров детали;
— изменение размеров детали;
![]() — допускаемая величина этого изменения.
— допускаемая величина этого изменения.
Расчет по условию жесткости всегда следует дополнять расчетом на прочность.
Лекция 2. Геометрические характеристики плоских сечений.
Основным объектом, изучаемым в курсе сопротивление материалов, является стержень.
Сопротивление стержня различным видам деформации часто зависит не только от его материалов и размеров, но и от очертаний оси, формы поперечных сечений и их расположения. Рассмотрим основные геометрические характеристики поперечных сечений бруса, определяющие сопротивление различным видам деформаций. Так или иначе, проститутки Киева помогают многим мужчинам познать запретное удовольствие, которое они недополучают дома.
Статические моменты площади. Центр тяжести площади.
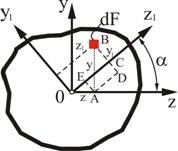
Рассмотрим произвольную фигуру (поперечное сечение бруса), связанную с координатными осями ![]() и
и ![]() (рис. 2.1). Выделим элемент площади
(рис. 2.1). Выделим элемент площади ![]() с координатами
с координатами ![]() ,
, ![]() . По аналогии с выражением для момента силы относительно какой-либо оси можно составить выражения и для момента площади, которое называется моментом площади. Так, произведение элемента площади
. По аналогии с выражением для момента силы относительно какой-либо оси можно составить выражения и для момента площади, которое называется моментом площади. Так, произведение элемента площади ![]() на расстояние
на расстояние ![]() от оси
от оси ![]() .
.
называется статическим моментом элемента площади относительно оси ![]() .
.
Рис. 2.1
Аналогично:
Просуммировав такие произведения по всей площади фигуры, получим соответственно статические моменты относительно осей ![]() и
и ![]() :
:
Пусть ![]() ,
, ![]() - координаты центра тяжести фигуры. Продолжая аналогию с моментами сил, на основании теоремы о моменте равнодействующей можно написать следующие выражения:
- координаты центра тяжести фигуры. Продолжая аналогию с моментами сил, на основании теоремы о моменте равнодействующей можно написать следующие выражения:
где ![]() - площадь фигуры. Очевидно, что статические моменты площади относительно осей проходящих через центр тяжести (центральных осей) равны нулю.
- площадь фигуры. Очевидно, что статические моменты площади относительно осей проходящих через центр тяжести (центральных осей) равны нулю.
Координаты центра тяжести:
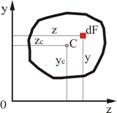
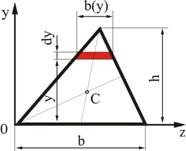
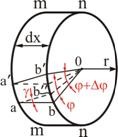
В качестве примера вычислим статический момент треугольника (рис. 2.2) относительно оси, проходящей через основание. На расстоянии ![]() от нее выделим элементарную площадку в виде полоски, параллельной оси
от нее выделим элементарную площадку в виде полоски, параллельной оси ![]() . Площадь полоски
. Площадь полоски
Учитывая, что
имеем
Рис. 2.2
Еще проще решить эту задачу, пользуясь формулой (2.4).
Учитывая, что
статический момент
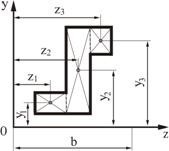
Для вычисления статических моментов сложной фигуры ее разбивают на простые части (рис. 2.3), для каждой из которых известна площадь ![]() и положение центра тяжести
и положение центра тяжести ![]() и
и ![]() . Статический момент площади всей фигуры относительно данной оси определяется как сумма статических моментов каждой части:
. Статический момент площади всей фигуры относительно данной оси определяется как сумма статических моментов каждой части:
Рис. 2.3
По формулам (2.5) и (2.6) легко найти координаты центра тяжести сложной фигуры:
Моменты инерции плоски фигур
Осевым, или экваториальным, моментом инерции площади фигуры называют интеграл произведений элементарных площадей на квадраты расстояний от рассматриваемой оси
Рис. 2.4
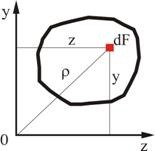
Полярным моментом инерции площади фигуры относительно данной точки (полюса ![]() ) называют интеграл произведений элементарных площадей на квадраты их расстояний от полюса:
) называют интеграл произведений элементарных площадей на квадраты их расстояний от полюса:
Если через полюс проведена система взаимно перпендикулярных осей ![]() и
и ![]() , то
, то ![]() . Из выражения (2.9) имеем
. Из выражения (2.9) имеем
Отметим, что величины осевых и полярных моментов инерции всегда положительны.
Центробежным моментом инерции называют интеграл произведений площадей элементарных площадок на их расстояния от координатных осей ![]() и
и ![]() :
:
В зависимости от положения осей центробежный момент инерции может быть положительным или отрицательным. Очевидно, что, постепенно поворачивая оси, можно найти такое их положение, при котором центробежный момент инерции равен нулю. Такие оси называют главными осями инерции.
Две взаимно перпендикулярные оси, из которых хотя бы одна является осью симметрии фигуры, всегда будут ее главными осями инерции
Главные оси, проходящие через центр тяжести сечения, называют главными центральными осями.
Моменты инерций сложных сечений, моменты инерций относительно параллельных осей
В расчетной практике часто приходится вычислять моменты инерции сложных сечений относительно различных осей, лежащих в плоскости фигуры. Для стандартных поперечных сечений стержней моменты инерции относительно различных осей даны в сортаменте.
При вычислении нестандартных сложных сечений последние можно разбить на отдельные простые части, моменты которых известны. Из основного свойства интеграла суммы следует, что момент инерции сложной фигуры равен сумме моментов инерции составных ее частей.
Если в сечении есть отверстие, его обычно удобно считать частью фигуры с отрицательной площадью.
Моменты инерций относительно параллельных осей.
Пусть известны моменты инерции фигуры относительно центральных осей ![]() и
и ![]() :
:
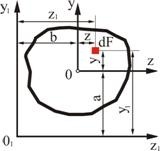
Требуется определить моменты инерции относительно осей, параллельных центральным (рис 2.5).
Рис. 2.5
Координаты любой точки в новой системе ![]() можно выразить через координаты в старых осях так:
можно выразить через координаты в старых осях так:
Подставим эти значения в формулы (2.13) и интегрируем почленно:
Так как интегралы ![]() и
и ![]() равны нулю как статические моменты относительно центральных осей, то формулы (2.14) — (2.16) принимают вид
равны нулю как статические моменты относительно центральных осей, то формулы (2.14) — (2.16) принимают вид
Зависимости между моментами инерции при повороте координатных осей.
Пусть известны моменты инерции произвольной фигуры (рис. 2. 6) относительно координатных осей ![]() ,
,![]() :
:
Повернем оси ![]() ,
,![]() на угол
на угол ![]() против часовой стрелки, считая угол поворота осей в этом направлении положительным.
против часовой стрелки, считая угол поворота осей в этом направлении положительным.
Рис. 2.6
Найдем теперь моменты инерции сечения относительно повернутых осей ![]() ,
,![]() :
:
Координаты произвольной элементарной площадки в новой системе ![]()
![]() выражаются через координаты
выражаются через координаты ![]() ,
,![]() прежней системы следующим образом:
прежней системы следующим образом:
Подставив эти выражения в (2.19) окончательно получим:
Складывая почленно формулы (2.22),(2.23), находим
При повороте прямоугольных осей сумма моментов инерции не изменяется и равна полярному моменту инерции относительно начала координат.
Определение направления главных осей. Главные моменты инерции.
Наиболее практическое значение имеют главные центральные оси, центробежный момент инерции относительно которых равен нулю. Будем обозначать такие оси буквами ![]() и
и ![]() .
.
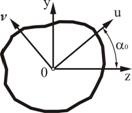
Чтобы определить положение главных центральных осей несимметричной фигуры, повернем произвольную начальную систему центральных осей ![]() ,
,![]() (рис 2.7) на некоторый угол
(рис 2.7) на некоторый угол ![]() при котором центробежный момент инерции становится равным нулю:
при котором центробежный момент инерции становится равным нулю:
Рис. 2.7
Согласно формулы (2.24)
откуда
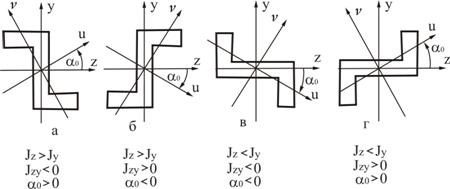
Полученные из формулы (2.28) два значения угла ![]() отличаются друг от друга на 90° и дают положение главных осей. Как легко видеть, меньший из этих углов по абсолютной величине не превышает π/4. В дальнейшем будем пользоваться только меньшим углом. Проведенную под этим углом главную ось будем обозначать буквой
отличаются друг от друга на 90° и дают положение главных осей. Как легко видеть, меньший из этих углов по абсолютной величине не превышает π/4. В дальнейшем будем пользоваться только меньшим углом. Проведенную под этим углом главную ось будем обозначать буквой ![]() . На рис (2.8) приведены некоторые примеры обозначения главных осей в соответствии с указанным правилом. Начальные оси обозначаются буквами
. На рис (2.8) приведены некоторые примеры обозначения главных осей в соответствии с указанным правилом. Начальные оси обозначаются буквами ![]() и
и ![]() .
.
Рис. 2.8
Значения главных моментов инерции можно определить из следующих выражений:
Причем верхние знаки следует брать при ![]() >
>![]() , а нижние – при
, а нижние – при ![]() <
<![]() .
.
Понятие о радиусе инерции
Момент инерции фигуры относительно какой-либо оси можно представить в виде произведения площади фигуры на квадрат некоторой величины, называемой радиусом инерции.
где ![]() - радиус инерции относительно оси
- радиус инерции относительно оси ![]() .
.
Из выражения (2.31) следует, что
Аналогично радиус инерции площади сечения относительно оси ![]()
Главным центральным осям инерции соответствуют главные радиусы инерции
Лекция 4. Теории прочности. Чистый сдвиг
Лекция 4. Теории прочности. Чистый сдвиг{jcomments on}
Теории прочности.
Важнейшей задачей инженерного расчета является оценка прочности элемента конструкции по известному напряженному состоянию. Для простых видов деформаций, в частности для одноосных напряженных состояний, определение значений опасных напряжений не представляет особых трудностей. Вспомним, что под опасными напряжениями понимают напряжения, соответствующие началу разрушения (при хрупком состоянии материала) или появлению остаточных деформаций (в случае пластического состояния материала):
По опасным напряжениям устанавливают допускаемые напряжения, обеспечивающие определенный запас против наступления предельного состояния.
При сложном напряженном состоянии, как показывают опыты, опасное состояние может иметь место при различных значениях главных напряжений ![]() ,
, ![]() ,
, ![]() в зависимости от соотношений между ними. В этом случае вводят гипотезу о преимущественном влиянии на прочность материала того или иного фактора. Предельное значение фактора, определяющего прочность, находят на основании простых опытов (на растяжение, сжатие, кручение).
в зависимости от соотношений между ними. В этом случае вводят гипотезу о преимущественном влиянии на прочность материала того или иного фактора. Предельное значение фактора, определяющего прочность, находят на основании простых опытов (на растяжение, сжатие, кручение).
Выбранная указанным образом гипотеза называется механической теорией прочности.
Рассмотрим классические теории прочности.
Первая теория прочности (критерий наибольших нормальных напряжений).
Согласно этой теории, преимущественное влияние на прочность оказывает величина наибольшего нормального напряжения.
Критерий наибольших нормальных напряжений из трех главных напряжений учитывает только одно — наибольшее, полагая, что два других не влияют на прочность.
Условие прочности согласно первой теории прочности следующее:
где ![]() - допускаемое напряжение при растяжении,
- допускаемое напряжение при растяжении, ![]() - допускаемое напряжение при сжатии.
- допускаемое напряжение при сжатии.
Данная теория дает удовлетворительные результаты лишь для весьма хрупких материалов (камень, керамика, инструментальные стали и т. п.).
Вторая теория прочности (критерий наибольших линейных деформаций).
Данная теория предполагает, что нарушение прочности в общем случае напряженного состояния наступает тогда, когда наибольшая линейная деформация ![]() достигает своего максимального значения.
достигает своего максимального значения.
Условие прочности согласно второй теории прочности принимает следующий вид:
или
Опытная проверка этой теории указывает на удовлетворительные результаты лишь для хрупкого состояния материала (легированный чугун, высокопрочные стали после низкого отпуска).
Третья теория прочности (критерий наибольших касательных напряжений).
Согласно этой теории предполагается, что предельное состояние в общем случае наступает тогда, когда наибольшее касательное напряжение ![]() достигает опасного значения
достигает опасного значения
Условие прочности согласно третьей теории прочности принимает следующий вид: ![]()
Третья теория прочности хорошо подтверждается опытами для материалов, одинаково работающих на растяжение и на сжатие.
Четвертая теория прочности (критерий удельной потенциальной энергии формоизменения).
Согласно этой теории, опасное состояние (текучесть) в общем случае наступает тогда, когда удельная потенциальная энергия формоизменения достигает своего предельного значения.
Условие прочности согласно четвертой теории прочности принимает следующий вид: ![]()
Опыты хорошо подтверждают четвертую теорию прочности для пластичных материалов, одинаково работающих на растяжение и на сжатие.
Сдвиг
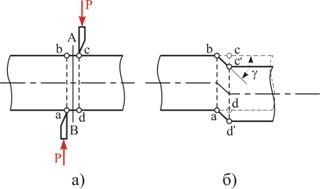
Если на брус действуют две равные силы ![]() , весьма близко расположенные друг к другу, перпендикулярные к оси бруса и направленные в противоположные стороны, как это бывает при разрезании прутков ножницами (рис. 4.1, а), то при достаточной величине сил происходит срез.
, весьма близко расположенные друг к другу, перпендикулярные к оси бруса и направленные в противоположные стороны, как это бывает при разрезании прутков ножницами (рис. 4.1, а), то при достаточной величине сил происходит срез.
Рис. 4.1
Левая часть тела отделяется от правой по некоторому сечению ![]() . Деформация, предшествующая срезу, которая заключается в перекашивании прямых углов элементарного параллелепипеда, называется сдвигом. На рис. 4.1, б показан сдвиг, происходящий в параллелепипеде до среза; прямоугольник
. Деформация, предшествующая срезу, которая заключается в перекашивании прямых углов элементарного параллелепипеда, называется сдвигом. На рис. 4.1, б показан сдвиг, происходящий в параллелепипеде до среза; прямоугольник ![]() превращается в параллелограмм
превращается в параллелограмм ![]() . Величина
. Величина ![]() , на которую сечение
, на которую сечение ![]() сдвинулось относительно соседнего сечения
сдвинулось относительно соседнего сечения ![]() , называется абсолютным сдвигом. Угол
, называется абсолютным сдвигом. Угол ![]() , на который изменяются прямые углы параллелепипеда, называется относительным сдвигом.
, на который изменяются прямые углы параллелепипеда, называется относительным сдвигом.
С учетом малости деформаций угол ![]() можно определить следующим образом:
можно определить следующим образом:
Очевидно, что в сечении ![]() из шести внутренних силовых факторов будет возникать только поперечная сила
из шести внутренних силовых факторов будет возникать только поперечная сила ![]() , равная силе
, равная силе ![]()
Принимая, что касательные напряжения равномерно распределены по площади поперечного сечения ![]() , их значения можно определить по формуле
, их значения можно определить по формуле
Допущение о равномерности распределения касательных напряжений по сечению весьма условно. Однако это допущение во многих случаях себя оправдывает и поэтому в инженерной практике им широко пользуются при расчете болтов, заклепочных соединений, шпонок, сварных соединений и других деталей.
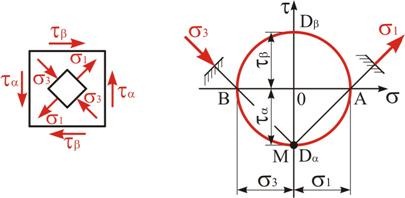
При расчете ряда элементов конструкций встречается частный случай плоского напряженного состояния, когда на четырех гранях прямоугольного элемента действуют только касательные напряжения (рис 4.2). Такое напряженное состояние называется чистым сдвигом.
Воспользуемся построением круга напряжений для определения величины и направления главных напряжений.
Рис. 4.2
Поскольку в данном случае
находим, что главные площадки в данном случае наклонены к граням элемента под углом 45°, а главные напряжения равны
Проверим прочность элемента, испытывающего деформацию чистого сдвига.
Условие прочности составим по второй, третьей и четвертой теориям прочности:
а) по второй теории:
Подставляя значения главных напряжений, находим
Правая часть выражения представляет собой допускаемое напряжение при чистом сдвиге:
Для металлов ![]() . Следовательно, по второй теории прочности
. Следовательно, по второй теории прочности
б) по третьей теории:
Подставляя значения главных напряжений, находим
Т.е допускаемое напряжение при сдвиге по третьей теории
б) по четвертой теории:
Подставляя значения главных напряжений, находим
Следовательно, по четвертой теории прочности
Полученные величины допускаемых напряжений применяют также при расчетах на прочность деталей, испытывающих деформацию среза. Для пластичных материалов наиболее подходит формула (4.15). Например, для стали марки Ст3 допускаемое напряжение на растяжение и сжатие ![]() МПа. Тогда
МПа. Тогда
Условие прочности на сдвиг (срез) может быть записано в обычном виде:
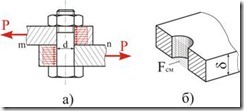
В качестве примера рассмотрим расчет болтового соединения, приведенного на рис. 4.3.
Рис. 4.3
Силы ![]() стремятся сдвинуть листы относительно друг друга. Этому препятствует болт, на который со стороны каждого листа передаются распределенные по контактной поверхности силы, равнодействующие которых равны
стремятся сдвинуть листы относительно друг друга. Этому препятствует болт, на который со стороны каждого листа передаются распределенные по контактной поверхности силы, равнодействующие которых равны ![]() . Усилия стремятся срезать болт в плоскости раздела листов
. Усилия стремятся срезать болт в плоскости раздела листов ![]() , так как в этом сечении действует максимальная поперечная сила
, так как в этом сечении действует максимальная поперечная сила ![]() . Считая, что касательные напряжения распределены равномерно, получим
. Считая, что касательные напряжения распределены равномерно, получим
Таким образом, условие прочности болта на срез принимает вид
Отсюда можно найти диаметр болта:
При расчете болтовых, заклепочных и других соединений следует учитывать, что нагрузки, приложенные к элементам соединений, помимо среза вызывают смятие контактирующих поверхностей. Под смятием понимают пластическую деформацию, возникающую на поверхностях контакта
Максимальное напряжение смятия на цилиндрических поверхностях
где ![]() представляет собой площадь проекции поверхности контакта на диаметральную плоскость (рис.4.3)
представляет собой площадь проекции поверхности контакта на диаметральную плоскость (рис.4.3)
Условие прочности на смятие имеет вид:
Допускаемые напряжения на смятие устанавливают опытным путем и принимают равным ![]() .
.
На основании зависимости (4.21) получим
Чтобы были удовлетворены условия прочности на срез и на смятие, из двух найденных диаметров следует взять больший, округлив его до стандартного значения.
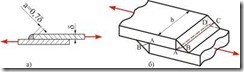
На срез принято рассчитывать и некоторые сварные соединения.
Рис. 4.4
Если не учитывать наплывы, то в разрезе угловой шов имеет форму равнобедренного прямоугольного треугольника (рис. 4.4, а). Разрушение шва будет происходить по его минимальному сечению ![]() (рис. 4.4, б), высота которого
(рис. 4.4, б), высота которого
Для нахлесточного соединения в расчет вводят оба шва. Запишем условие прочности шва:
где ![]() - расчетная длина торцевого шва;
- расчетная длина торцевого шва;
![]() - допускаемое напряжение для сварных соединений.
- допускаемое напряжение для сварных соединений.
Поскольку в начале и в конце шва из-за непровара качество ухудшается, действительную его длину увеличивают по сравнению с расчетной на 10 см. ![]() ,
,
где ![]() - действительная длина шва (на рис. 4.4, б
- действительная длина шва (на рис. 4.4, б ![]() )
)
Закон Гука при сдвиге.
Для определения зависимости между нагрузкой и деформацией при сдвиге проводят испытания материала на кручение. При данном испытании строится диаграмма сдвига ![]() (график зависимости между касательным напряжением и относительным сдвигом). Более подробное описание испытания на кручение образцов цилиндрической формы приведено в методических указаниях к лабораторным работам
(график зависимости между касательным напряжением и относительным сдвигом). Более подробное описание испытания на кручение образцов цилиндрической формы приведено в методических указаниях к лабораторным работам
Для пластичных материалов диаграмма сдвига аналогична диаграмме растяжения (рис. 4.5).
Рис. 4.5
При рассмотрении деформации образца в пределах упругости видна линейная зависимость между относительным сдвигом ![]() и касательным напряжением.
и касательным напряжением.
где ![]() - коэффициент пропорциональности, который называется модулем упругости при сдвиге или модулем упругости второго рода.
- коэффициент пропорциональности, который называется модулем упругости при сдвиге или модулем упругости второго рода.
Зависимость (4.24) выражает закон Гука при сдвиге.
Между величинами модуля продольной упругости ![]() и модуля упругости при сдвиге
и модуля упругости при сдвиге ![]() для одного и того же материала существует зависимость
для одного и того же материала существует зависимость
При значении коэффициента Пуассона ![]() получим, что
получим, что
Запишем выражение для перемещения одной грани относительно другой (абсолютного сдвига![]() (рис. 4.1)) при чистом сдвиге. Обозначая площадь грани
(рис. 4.1)) при чистом сдвиге. Обозначая площадь грани ![]() , равнодействующую сдвигающую силу
, равнодействующую сдвигающую силу ![]() и расстояние между сдвигаемыми гранями
и расстояние между сдвигаемыми гранями ![]() (рис. 4.1), получим
(рис. 4.1), получим
Формула (4.26) выражает закон Гука для абсолютного сдвига.
Лекция 3. Основы теории напряженного состояния.
Лекция 3. Основы теории напряженного состояния.{jcomments on}
Напряжения в точке.
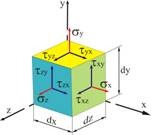
Если мысленно вырезать вокруг какой-нибудь точки тела элемент в виде бесконечного малого кубика, то по его граням в общем случае будут действовать напряжения, представленные на рис. 3.1.
Совокупность нормальных и касательных напряжений, действующих по всем площадкам (сечениям), содержащим какую-либо точку называют напряженным состоянием тела в данной точке
Рис. 3.1
Таким образом, на гранях элементарного параллелепипеда, выделенного в окрестности точки нагруженного тела, действуют девять компонентов напряжения. Запишем их в виде следующей квадратной матрицы:
где в первой, второй и третьей строках расположены составляющие напряжений соответственно на площадках, перпендикулярных к осям ![]() ,
, ![]() ,
, ![]() . Эта совокупность напряжений называется тензором напряжений.
. Эта совокупность напряжений называется тензором напряжений.
Закон парности касательных напряжений. Главные площадки и главные напряжения.
Составим уравнение моментов всех сил, приложенных к элементарному параллелепипеду относительно оси ![]() . (рис. 3.1.).
. (рис. 3.1.).
Силы, параллельные этой оси и пересекающие ее, в уравнение не войдут. Моменты сил ![]() на двух гранях, перпендикулярных оси
на двух гранях, перпендикулярных оси ![]() , уравновешиваются, равно как и моменты сил
, уравновешиваются, равно как и моменты сил ![]() на верхней и нижней гранях элемента. Таким образом, получаем:
на верхней и нижней гранях элемента. Таким образом, получаем:
Аналогично из двух других уравнений находим:
Итак, имеем равенства
называемые законом парности касательных напряжений
Закон парности касательных напряжений — касательные напряжения на двух любых, но взаимно перпендикулярных площадках, направленные перпендикулярно к линии пересечения площадок, равны по величине. При этом они стремятся повернуть элемент в разные стороны.
При изменении ориентации граней выделенного элемента меняются также действующие на его гранях напряжения. Можно провести такие площадки, на которых касательные напряжения равны нулю. Площадки, на которых касательные напряжения равны нулю, называются главными площадками, а нормальные напряжения на этих площадках — главными напряжениями.
Можно доказать, что в каждой точке напряженного тела существует три главные взаимно перпендикулярные площадки.
Главные напряжения обозначают ![]() ,
, ![]() ,
, ![]() . При этом индексы следует расставлять так, чтобы выполнялось неравенство
. При этом индексы следует расставлять так, чтобы выполнялось неравенство
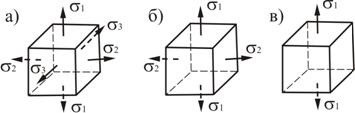
Если отличны от нуля все три главных напряжения, то напряженное состояние называется трехосным или объемным (рис.3.2, а).
Если равно нулю одно из главных напряжения, то напряженное состояние называется двухосным или плоским (рис.3.2, б).
Если равно нулю два главных напряжения, то напряженное состояние называется одноосным или линейным (рис.3.2, в).
Рис. 3.2
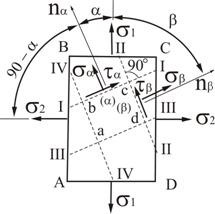
Плоское напряженное состояние.
При исследовании напряженного состояния элементов конструкций наиболее часто приходится иметь дело с плоским напряженным состоянием. Оно встречается при кручении, изгибе и сложном сопротивлении. Поэтому на нем мы остановимся несколько подробнее.
Рассмотрим элемент, грани которого являются главными площадками.
Рис. 3.3
По ним действуют положительные напряжения ![]() и
и ![]() , а третье главное напряжение
, а третье главное напряжение ![]() (направление
(направление ![]() перпендикулярно к плоскости чертежа).
перпендикулярно к плоскости чертежа).
Проведем сечение I — I, которое определит площадку (![]() ), характеризуемую положительным углом
), характеризуемую положительным углом ![]() . Напряжения
. Напряжения ![]() и
и ![]() по этой площадке будут определяться по формулам:
по этой площадке будут определяться по формулам:
Сжимающие главные напряжения подставляют в эти формулы со знаком «минус», а угол ![]() отсчитывают от алгебраически большего главного напряжения.
отсчитывают от алгебраически большего главного напряжения.
Проведем сечение II — II, которое определит площадку ![]() , перпендикулярную площадке
, перпендикулярную площадке ![]() . Нормаль
. Нормаль ![]() к ней образует с направлением
к ней образует с направлением ![]() угол
угол ![]()
Подставив в формулы (3.2) и (3.3) значения угла ![]() , будем иметь
, будем иметь
Совокупность формул (3.2) — (3.5) дает возможность находить напряжения по любым взаимно перпендикулярным наклонным площадкам, если известны главные напряжения.
Складывая равенства (3.2) и (3.4), обнаруживаем, что
т. е. сумма нормальных напряжений по двум взаимно перпендикулярным площадкам не зависит от угла наклона этих площадок и равна сумме главных напряжений.
Из формул (3.3) и (3.5) видим, что касательные напряжения достигают наибольшей величины при ![]() , т. е. по площадкам, наклоненным к главным площадкам под углом
, т. е. по площадкам, наклоненным к главным площадкам под углом ![]() , причем
, причем
Сравнивая формулы (3.3) и (3.5), находим, что
Это равенство выражает закон парности касательных напряжений.
Проведем теперь еще два сечения (рис. 3.3): Сечение ІІІ — ІІІ, параллельное І — І, и сечение ІV – ІV, параллельное ІІ — ІІ. Элемент ![]() , выделенный четырьмя сечениями из элемента
, выделенный четырьмя сечениями из элемента ![]() (рис. 3.4, а), будет иметь вид, показанный на рис 3.4, б. Оба элемента определяют одно и то же напряженное состояние, но элемент
(рис. 3.4, а), будет иметь вид, показанный на рис 3.4, б. Оба элемента определяют одно и то же напряженное состояние, но элемент ![]() представляет его главными напряжениями, а элемент
представляет его главными напряжениями, а элемент ![]() - напряжениями на наклонных площадках.
- напряжениями на наклонных площадках.
Рис. 3.4
В теории напряженного состояния можно разграничить две основные задачи.
Прямая задача. В точке известны положения главных площадок и соответствующие им главные напряжения; требуется найти нормальные и касательные напряжения по площадкам, наклоненным под заданным углом ![]() к главным.
к главным.
Обратная задача. В точке известны нормальные и касательные напряжения, действующие в двух взаимно перпендикулярных площадках; требуется найти главные направления и главные напряжения. Обе задачи можно решать как аналитически, так и графически.
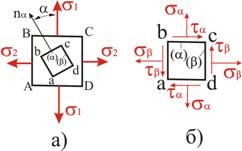
Прямая задача в плоском напряженном состоянии. Круг напряжений (круг Мора).
Аналитическое решение прямой задачи дается формулами (3.2) — (3.5).
Проанализируем напряженное состояние, воспользовавшись простым графическим построением. Для этого введем в рассмотрение геометрическую плоскость и отнесем ее к прямоугольным координатным осям ![]() и
и ![]() . Порядок расчета опишем на примере напряженного состояния, изображенного на рис. 3.5, а.
. Порядок расчета опишем на примере напряженного состояния, изображенного на рис. 3.5, а.
Выбрав для напряжений некоторый масштаб, откладываем на оси абсцисс (рис 3.5, б) отрезки
На ![]() как на диаметре строим окружность с центром в точке
как на диаметре строим окружность с центром в точке ![]() . Построенный круг носит название круга напряжений или круга Мора.
. Построенный круг носит название круга напряжений или круга Мора.
Рис. 3.5
Координаты точек круга соответствуют нормальным и касательным напряжениям на различных площадках. Так, для определения напряжения на площадке, проведенной под углом ![]() (рис. 3.5, а) из центра круга
(рис. 3.5, а) из центра круга ![]() (рис 3.5, б) проводим луч под углом
(рис 3.5, б) проводим луч под углом ![]() до пересечения с окружностью в точке
до пересечения с окружностью в точке ![]() (положительные углы откладываем против часовой стрелки). Абсцисса точки (отрезок
(положительные углы откладываем против часовой стрелки). Абсцисса точки (отрезок ![]() ) равна нормальному напряжению
) равна нормальному напряжению ![]() , а ордината ее (отрезок
, а ордината ее (отрезок ![]() ) — касательному напряжению
) — касательному напряжению ![]() .
.
Напряжение на площадке, перпендикулярной к рассмотренной, найдем, проведя луч под углом ![]() и получив в пересечении с окружностью точку
и получив в пересечении с окружностью точку ![]() . Очевидно, ордината точки
. Очевидно, ордината точки ![]() соответствует касательному напряжению
соответствует касательному напряжению ![]() , а абсцисса точки
, а абсцисса точки ![]() - нормальному напряжению
- нормальному напряжению ![]() .
.
Проведя из точки ![]() линию, параллельную
линию, параллельную ![]() (в нашем случае горизонталь), до пересечения с кругом, найдем полюс — точку
(в нашем случае горизонталь), до пересечения с кругом, найдем полюс — точку ![]() . Линия, соединяющая полюс с любой точкой круга, параллельна направлению нормального напряжения на площадке, которой эта точка соответствует. Так, например, линия
. Линия, соединяющая полюс с любой точкой круга, параллельна направлению нормального напряжения на площадке, которой эта точка соответствует. Так, например, линия ![]() параллельна главному напряжению
параллельна главному напряжению ![]() . Очевидно, что линия
. Очевидно, что линия ![]() параллельна направлению главного напряжения
параллельна направлению главного напряжения ![]() .
.
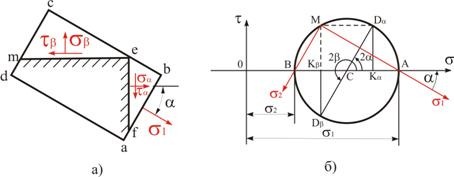
Обратная задача в плоском напряженном состоянии.
При практических расчетах обычно определяют нормальные и касательные напряжения на некоторых двух взаимно перпендикулярных площадках. Пусть, например, известны напряжения ![]() ,
, ![]() ,
, ![]() ,
, ![]() (рис. 3.6, а). По этим данным требуется определить величины главных напряжений и положение главных площадок.
(рис. 3.6, а). По этим данным требуется определить величины главных напряжений и положение главных площадок.
Сначала решим эту задачу графически. Примем, что ![]() >
>![]() , а
, а ![]() >
>![]() .
.
В геометрической плоскости в системе координат ![]() нанесем точку
нанесем точку ![]() , с координатами
, с координатами ![]() ,
, ![]() и точку
и точку ![]() с координатами
с координатами ![]() ,
,![]() (рис. 3.6, б). Соединив точки
(рис. 3.6, б). Соединив точки ![]() и
и ![]() , находим центр круга — точку
, находим центр круга — точку ![]() - и радиусом
- и радиусом ![]() проводим окружность. Абсциссы точек ее пересечения с осью
проводим окружность. Абсциссы точек ее пересечения с осью ![]() - отрезки
- отрезки ![]() и
и ![]() - дадут соответственно величины главных напряжений
- дадут соответственно величины главных напряжений ![]() и
и ![]() .
.
Для определения положения главных площадок найдем полюс и воспользуемся его свойством. Проведем из точки ![]() линию параллельно линии действия напряжения
линию параллельно линии действия напряжения ![]() , т. е. горизонталь. Точка
, т. е. горизонталь. Точка ![]() пересечения этой линии с окружностью и является полюсом. Соединяя полюс
пересечения этой линии с окружностью и является полюсом. Соединяя полюс ![]() с точками
с точками ![]() и
и ![]() , получим направления главных напряжений. Главные площадки перпендикулярны к найденным направлениям главных напряжений.
, получим направления главных напряжений. Главные площадки перпендикулярны к найденным направлениям главных напряжений.
Рис. 3.6
Используем построенный круг для получения аналитических выражений главных напряжений ![]() и
и ![]() :
:
Формула (3.10) определяет единственное значение угла ![]() , на который нужно повернуть нормаль
, на который нужно повернуть нормаль ![]() , чтобы получить направление алгебраически большего главного напряжения. Отрицательному значению
, чтобы получить направление алгебраически большего главного напряжения. Отрицательному значению ![]() соответствует поворот по часовой стрелке.
соответствует поворот по часовой стрелке.
Если одно из главных напряжений окажется отрицательным, а другое положительным, то их следует обозначать ![]() и
и ![]() . Если оба главных напряжения окажутся отрицательными, то их следует обозначать
. Если оба главных напряжения окажутся отрицательными, то их следует обозначать ![]() и
и ![]() .
.
Лекция 5. Кручение. Кручение бруса некруглого сечения.
Лекция 5. Кручение. Кручение бруса некруглого сечения.
Кручение прямого круглого бруса.
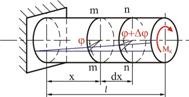
Деформация кручения вызывается парами сил, плоскости действия которых перпендикулярны к оси стержня. Поэтому при кручении в произвольном поперечном сечении стержня из шести внутренних силовых факторов возникает только один — крутящий момент ![]() . Как показывают опыты, поперечные сечения при кручении поворачиваются одно относительно другого вокруг оси стержня, при этом длина не меняется.
. Как показывают опыты, поперечные сечения при кручении поворачиваются одно относительно другого вокруг оси стержня, при этом длина не меняется.
Стержни, работающие на кручение, обычно называют валами.
Рассматривая кручение вала, легко установить, что под действием скручивающего момента любое сечение на расстоянии ![]() от заделки поворачивается относительно закрепленного сечения на некоторый угол
от заделки поворачивается относительно закрепленного сечения на некоторый угол ![]() - угол закручивания (Рис. 5.1). При этом чем больше скручивающий момент
- угол закручивания (Рис. 5.1). При этом чем больше скручивающий момент ![]() , тем больше и угол закручивания. Зависимости
, тем больше и угол закручивания. Зависимости ![]() , называемые диаграммами кручения, полученные для образца из пластичного материала, до некоторой степени подобны диаграммам растяжения (Рис. 5.2). В дальнейшем при выводе формул для напряжений и угла закручивания нас будет интересовать участок диаграммы кручения, соответствующий работе материала в пределах пропорциональности.
, называемые диаграммами кручения, полученные для образца из пластичного материала, до некоторой степени подобны диаграммам растяжения (Рис. 5.2). В дальнейшем при выводе формул для напряжений и угла закручивания нас будет интересовать участок диаграммы кручения, соответствующий работе материала в пределах пропорциональности.
Рассмотрим геометрическую картину деформации вала при кручении.
Если до деформации на поверхность вала нанести сетку, состоящую из линий, параллельных оси, и линий, представляющие собой параллельные круги, то после закручивания вала скручивающим моментом ![]() можно заметить следующее: образующие цилиндра превращаются в винтовые линии, параллельные круги не искривляются и расстояние между ними остается неизменным, радиусы, проведенные в торцевых сечениях остаются прямыми (Рис. 5.3). Полагая, что картина, наблюдаемая на поверхности вала, сохраняется и внутри, сформулируем гипотезы, взятые в основу теории кручения круглых стержней:
можно заметить следующее: образующие цилиндра превращаются в винтовые линии, параллельные круги не искривляются и расстояние между ними остается неизменным, радиусы, проведенные в торцевых сечениях остаются прямыми (Рис. 5.3). Полагая, что картина, наблюдаемая на поверхности вала, сохраняется и внутри, сформулируем гипотезы, взятые в основу теории кручения круглых стержней:
1. Поперечные сечения, плоские и нормальные к оси вала до деформации, остаются плоскими и нормальными к той же оси и после деформации.
На основании принятых гипотез кручение круглого вала можно представить как результат сдвигов, вызванных взаимным поворотом поперечных сечений относительно друг друга. Вследствие этого в поперечных сечениях возникают только касательные напряжения, а нормальные напряжения равны нулю.
Выделим из закручиваемого вала диск радиуса ![]() на расстоянии
на расстоянии ![]() от закрепленного конца, ограниченный двумя смежными сечениями
от закрепленного конца, ограниченный двумя смежными сечениями ![]() и
и ![]() , находящимися друг от друга на расстоянии
, находящимися друг от друга на расстоянии ![]() (Рис. 5.1) и рассмотрим его отдельно (Рис. 5.4)
(Рис. 5.1) и рассмотрим его отдельно (Рис. 5.4)
Проведем от точки ![]() прямую
прямую ![]() , параллельную
, параллельную![]() и соединим центр сечения
и соединим центр сечения ![]() с точкой
с точкой ![]() . Тогда угол
. Тогда угол ![]() , равный
, равный ![]() , будет углом поворота сечения
, будет углом поворота сечения ![]() относительно сечения
относительно сечения ![]() . У элемента
. У элемента ![]() до поворота сечения
до поворота сечения ![]() относительно сечения
относительно сечения ![]() верхняя и нижняя стороны были расположены горизонтально. После поворота стороны наклонились и приняли положение
верхняя и нижняя стороны были расположены горизонтально. После поворота стороны наклонились и приняли положение ![]() и
и ![]() . Следовательно, элемент претерпел абсолютный сдвиг, равный длине дуги:
. Следовательно, элемент претерпел абсолютный сдвиг, равный длине дуги:
Относительный сдвиг будет равен:
Отношение ![]() представляет относительный угол закручивания
представляет относительный угол закручивания ![]() (угол закручивания на единицу длины бруса). Тогда
(угол закручивания на единицу длины бруса). Тогда
Из этой формулы видно, что относительный сдвиг пропорционален радиусу закручиваемого цилиндрического тела.
На основании закона Гука для сдвига
Можно определить касательное напряжение для элементов лежащих на поверхности вала
Учитывая предположение, что деформация элементов на поверхности вала подобна деформации элементов внутри вала, для произвольного элемента, находящегося на расстоянии ![]() от центра поперечного сечения (рис 5.5)
от центра поперечного сечения (рис 5.5)
|
Рис. 5.5 |
Касательная элементарная сила на площадке Момент элементарной силы относительно оси бруса будет: |
Сумма таких элементарных моментов, распределенных по всему поперечному сечению ![]() , при равновесии, наступающем после деформации, должна быть равна крутящему моменту:
, при равновесии, наступающем после деформации, должна быть равна крутящему моменту:
Вынесем постоянные за знак интеграла, получим
Интеграл ![]() является полярным моментом инерции
является полярным моментом инерции ![]() (лекция 2, выражение (2.9)). Тогда
(лекция 2, выражение (2.9)). Тогда
Откуда относительный угол закручивания
Подставляя в выражение (5.5) выражение относительного угла закручивания получим
Это уравнение показывает, что напряжения в площадках сечения прямо пропорциональны их расстояниям до центра сечения.
При расчете на прочность при кручении необходимо знать максимальные напряжения для сравнения их с допускаемыми напряжениями. Очевидно, что максимальные напряжения при кручении круглого вала будут иметь точки максимально удаленные от оси вала. Т. е. точки с полярной координатой, равной радиусу сечения вала ![]()
Отношение полярного момента инерции![]() к наибольшему радиусу сечения
к наибольшему радиусу сечения ![]() называется полярным моментом сопротивления
называется полярным моментом сопротивления![]()
Тогда условие прочности при кручении будет иметь следующий вид
Для сплошного круглого сечения
Помимо расчета на прочность валы рассчитывают и на жесткость, ограничивая относительный угол закручивания некоторой допускаемой величиной ![]() :
:
Определение крутящего момента и построение эпюр крутящих моментов.
Для определения напряжений и деформаций произвольного вала необходимо знать величину крутящих моментов на его отдельных участках.
Крутящий момент ![]() в произвольном сечении вала равен сумме внешних моментов
в произвольном сечении вала равен сумме внешних моментов ![]() , расположенных по одну сторону сечения.
, расположенных по одну сторону сечения.
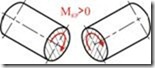
Крутящий момент ![]() считается положительным, если при наблюдении с торца вдоль оси рассматриваемой части он стремится вращать сечение по часовой стрелке (рис. 5.6).
считается положительным, если при наблюдении с торца вдоль оси рассматриваемой части он стремится вращать сечение по часовой стрелке (рис. 5.6).
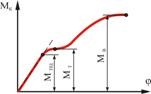
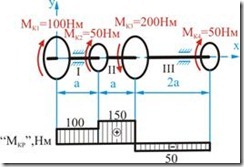
Рассмотрим в качестве примера построение эпюры крутящих моментов для трансмиссионного вала (рис. 5.7)
|
Рис. 5.6 |
Рис. 5.7 |
Разбиваем вал на участки ![]() ,
, ![]() ,
, ![]() .
.
Проведя произвольное сечение на первом участке:
Для второго участка:
На третьем участке рассматриваем правую часть от сечения, в котором определяем ![]() :
:
Построенная эпюра показывает, что хотя к валу и приложен момент ![]() Н·м, наибольший крутящий момент в сечении равен лишь
Н·м, наибольший крутящий момент в сечении равен лишь ![]() Н·м. Эту величину и следует использовать при расчете на прочность и жесткость.
Н·м. Эту величину и следует использовать при расчете на прочность и жесткость.
На практике часто бывают заданы не моменты, приложенные к дискам (шкивам или зубчатым колесам), а передаваемые мощности ![]() , Вт, и частота вращения вала
, Вт, и частота вращения вала ![]() . Запишем зависимость между этими величинами.
. Запишем зависимость между этими величинами.
В старой технической литературе использовалась единица мощности — лошадиная сила (1 л. с. ≈ 736 Вт). Если передаваемая мощность равна ![]() , л. с., то
, л. с., то
Расчет винтовых цилиндрических пружин с небольшим шагом
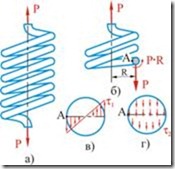
Пусть имеется винтовая цилиндрическая пружина с небольшим шагом витков, изготовленная из круглой проволоки и растягиваемая осевыми силами ![]() (рис. 5.8). Вследствие малости шага витков будем считать, что плоскости отдельных витков пружины перпендикулярны к оси пружины. Рассечем виток пружины плоскостью, проходящей через ось пружины. Удалим одну часть пружины и рассмотрим равновесие оставшейся части (рис. 5.8, б). Для равновесия необходимо приложить в центре сечения силу
(рис. 5.8). Вследствие малости шага витков будем считать, что плоскости отдельных витков пружины перпендикулярны к оси пружины. Рассечем виток пружины плоскостью, проходящей через ось пружины. Удалим одну часть пружины и рассмотрим равновесие оставшейся части (рис. 5.8, б). Для равновесия необходимо приложить в центре сечения силу ![]() , параллельную оси пружины и направленную вниз, и момент
, параллельную оси пружины и направленную вниз, и момент ![]() , где
, где ![]() — средний радиус витка пружины. Так как момент
— средний радиус витка пружины. Так как момент ![]() действует в плоскости сечения, то он вызывает в сечении напряжения кручения (рис. 5.8, в), максимальная величина которых на внешних волокнах равна:
действует в плоскости сечения, то он вызывает в сечении напряжения кручения (рис. 5.8, в), максимальная величина которых на внешних волокнах равна:
где ![]() - диаметр поперечного сечения проволоки.
- диаметр поперечного сечения проволоки.
Рис. 5.8
Сила ![]() , действующая в плоскости поперечного сечения, вызывает в нем напряжение сдвига, которое будем считать равномерно распределенным по сечению (рис. 5.8, г). Это напряжение будет равно:
, действующая в плоскости поперечного сечения, вызывает в нем напряжение сдвига, которое будем считать равномерно распределенным по сечению (рис. 5.8, г). Это напряжение будет равно:
Для определения суммарных напряжений на внешних волокнах проволоки пружины следует сложить геометрически напряжения ![]() и
и ![]() . Максимальное напряжение в сечении будет в той точке периферии сечения, в которой направления напряжений
. Максимальное напряжение в сечении будет в той точке периферии сечения, в которой направления напряжений ![]() и
и ![]() совпадут. Нетрудно видеть, что такой точкой будет точка А.
совпадут. Нетрудно видеть, что такой точкой будет точка А.
В этой точке напряжение будет равно:
Мы рассмотрели растяжение пружины; совершенно такой же результат получился бы при рассмотрении сжатия пружины. При расчете пружин, у которых средний радиус пружины R во много раз больше диаметра d проволоки, из которой она изготовлена, вторым слагаемым, стоящим в скобках, обычно пренебрегают. Для таких пружин формула (5.19) упрощается и принимает вид
При расчете пружины, помимо расчета на прочность, часто необходимо бывает определить удлинение или сжатие (осадку) пружины, т. е. ее деформацию![]() . Эта деформация, если принимать во внимание только кручение витков, будет определяться по формуле:
. Эта деформация, если принимать во внимание только кручение витков, будет определяться по формуле:
где ![]() - средний диаметр витка пружины;
- средний диаметр витка пружины;
Кручение стержней некруглого сечения
В инженерной практике довольно часто кручению подвергаются стержни, имеющие не круглое, а прямоугольное, треугольное, эллиптическое и другие сечения. В этих случаях гипотеза плоских сечений неприменима, так как сечения искривляются (депланируют). Точные расчеты стержней некруглого сечения можно получить методами теории упругости. Однако поскольку в настоящем курсе нет возможности их изложить, приведем здесь только некоторые окончательные результаты. Отметим при этом, что в стержнях произвольного сечения, как и в стержнях круглого сечения, касательные напряжения при кручении направлены по касательной к контуру.
Наибольшие касательные напряжения, погонные и полные углы закручивания по аналогии с кручением стержней круглого сечения принято определять по формулам
Здесь ![]() и
и ![]() — некоторые геометрические характеристики, которые условно называют моментом инерции при кручении и моментом сопротивления при кручении, см4 и см3 соответственно.
— некоторые геометрические характеристики, которые условно называют моментом инерции при кручении и моментом сопротивления при кручении, см4 и см3 соответственно.
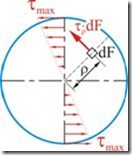
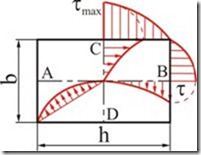
Наиболее часто встречается стержни прямоугольного сечения. В этом случае распределение касательных напряжений имеет вид, показанный на рис.5.9. Наибольшие напряжения возникают у поверхности посредине длинных сторон прямоугольного сечения (в точках С и D). Определяются они по формуле (5.22), где
Здесь ![]() - длинная сторона прямоугольного поперечного сечения;
- длинная сторона прямоугольного поперечного сечения;
Напряжения, возникающие у поверхности сечения посредине коротких сторон (в точках А и В), меньше. Их можно выразить через ![]() следующим образом:
следующим образом:
Рис. 5.9
Для определения относительного угла закручивания прямоугольного сечения в формуле (9.29) принимают
Коэффициенты ![]() ,
, ![]() и
и ![]() , зависящие от отношения
, зависящие от отношения ![]() , даны в табл. 5.1.
, даны в табл. 5.1.
Таблица 5.1
|
1 1,5 1,75 2,0 2,5 3,0 4,0 6,0 8,0 10,0 |
0,208 0,231 0,239 0,246 0,256 0,267 0,282 0,299 0,307 0,313 0,333 |
0,141 0,196 0,214 0,229 0,249 0,263 0,281 0,299 0,307 0,313 0,333 |
1 0,859 - 0,795 - 0,453 0,745 0,743 0,743 0,743 0,743 |
Запишем условия прочности и жесткости для прямоугольного сечения: