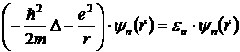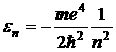Лекции для студентов

Глава II. Элементы зонной теории твердых тел.

§1. Энергетический спектр изолированных атомов.

Изолированные атомы представляют собой динамическую систему, состоящую из неподвижного ядра и вращающихся вокруг него электронов. Ирншоу доказал, что система точечных неподвижных зарядов находящихся, на конечных расстояниях друг от друга не является устойчивой системой, т.е. их потенциальная энергия не может иметь минимум, а атомы представляют собой устойчивую систему, следовательно, согласно теоремы Ирншоу они являются динамическими системами. Полная энергия атома равна , T — кинетическая энергия электронов, U — потенциальная энергия взаимодействия электронов с ядром и друг с другом. Для определенности рассмотрим атом с простейшей архитектурой — атом водорода (H), у него вокруг протона +1e вращается электрон –1e.

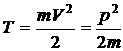, ; r — расстояние от электрона до центра ядра, U — имеет сферическую симметрию. Если , , то движение электрона e является связанным. Если , , то движение электрона e является свободным. Видно, что , .

Точную характеристику о состояниях электронов в атомах можно получить с помощью квантовой механики, учитывающую волновые свойства частиц. Состояния электронов в атомах можно описывать с помощью волновой функции, удовлетворяющей уравнению Шредингера . Однако в общем случае решение уравнения Шредингера это сложная задача, она легче решается для стационарных условиях электрона. Стационарная задача не описывает процессы, она описывает структуру системы в которой могут протекать процессы.

Полную волновую функцию электрона атома водорода в стационарном состоянии можно представить в виде произведения:

(1)

 — полная энергия электрона в n состоянии.

Амплитудная часть волновой функции должна удовлетворять стационарному уравнению Шредингера:

(2)

(3)

(4)

, n = 1,2,3… (5)

Из (4) следует, что атом водорода имеет дискретный спектр энергий, промежуточное состояние электрон принимать не может.

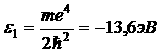. Состояние с такой энергией называется основным состоянием. В этом состоянии атом имеет максимальную устойчивость. А состояния с энергиями , называются возбужденными.

 — энергия ионизации водорода.

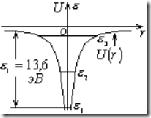
Соотношение (5) определяет энергию электрона в связанном состоянии, как видно эта энергия квантуется. Дискретность энергии связанного электрона является следствием проявления его волновых свойств. Движения такого электрона схожи со стоячей волной. Стоячая волна — это волна, получающаяся в результате интерференций двух одинаковых волн распространяющихся в противоположных направлениях. В связанном состоянии электронная волна распространяется в ограниченном объеме (в объеме атома). Как известно в этом случае стоячие волны могут иметь только определенное значение длин волн , .

Из последнего соотношения следует, что λ стоячих электромагнитных волн принимает ряд дискретных значений и следовательно, и энергия связанного электрона принимает ряд дискретных значений.

Движение свободного электрона можно описывать бегущей волной, распространяющейся в неограниченном пространстве, а бегущая волна может принимать любое значение λ, следовательно, энергия свободного электрона не квантуется.

Если электрон переходит из основного состояния в возбужденное , то он поглощает энергию: . Если электрон переходит из возбужденного состояния в основное, он испускает квант энергии .

Состояние электрона в атоме водорода с энергией имеет кратность вырождения равной 2n², n — основное квантовое число. Под кратностью вырождения следует понимать число различных состояний при данном значении энергии . Для электрона атома водорода, энергия зависит только от основного квантового числа n, следовательно, вырождение будет определяться числом различных значений орбитального (l), магнитного (m) и спинового (s) квантовых чисел.

В многоэлектронном атоме потенциальная энергия атома определяется не только взаимодействием электронов с ядром, но и взаимодействием друг с другом. В связи с этим энергия электронов зависит от дух квантовых чисел (n, l). Кратность вырождения состояния будет определяться числом различных квантовых чисел m и s. При данном квантовом числе l, кратность вырождения 2(2l+1).